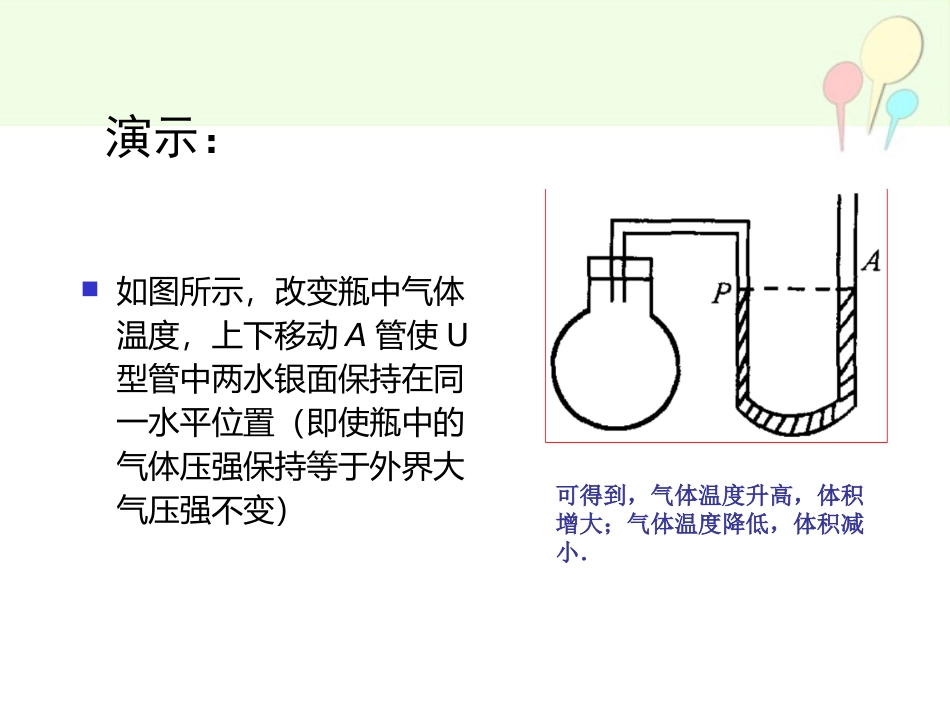
等压过程1.等压过程:气体在压强不变的情况下发生的状态变化过程叫做等压过程.2.一定质量气体的等压变化.演示:如图所示,改变瓶中气体温度,上下移动A管使U型管中两水银面保持在同一水平位置(即使瓶中的气体压强保持等于外界大气压强不变)可得到,气体温度升高,体积增大;气体温度降低,体积减小.3.盖·吕萨克定律:一定质量的某种气体,在压强不变的情况下,体积V与热力学温度成正比(VT).2211TVTVCTV可写成或(1)盖·吕萨克定律是实验定律,由法国科学家盖·吕萨克通过实验发现的.(2)成立条件:气体质量一定,压强不变.(3)在V/t=C中的C与气体的种类、质量、压强有关.注意:V正比于T而不正比于t,但Vt(4)一定质量的气体发生等压变化时,升高(或降低)相同的温度,增加(或减小)的体积是相同的.(5)解题时前后两状态的体积单位要统一.4.等压线(1)等压线:一定质量的某种气体在等压变化过程中,体积V与热力学温度T的正比关系在V-T直角坐标系中的图象叫做等压线.(2)一定质量气体的等压线的V-T图象,其延长线经过坐标原点,斜率反映压强大小,如图所示.(3)一定质量气体的等压线的物理意义①图线上每一个点表示气体一个确定的状态,同一根等压线上各状态的压强相同.②不同压强下的等压线,斜率越大,压强越小(同一温度下,体积大的压强小)如图所示p2<p1.体积为V=100cm3的空心球带有一根有刻度的均匀长管,管上共有N=101个刻度,设长管与球连接处为第一个刻度,以后顺序往上排列,相邻两刻度间管的体积为0.2cm3,水银液滴将球内空气与大气隔开,如图所示.当温度t=5℃时,水银液滴在刻度为N=21的地方.那么在此大气压下,能否用它测量温度?说明理由,若能,求其测量范围.(不计热膨胀).解析:首先应明确气体做等压变化,符合盖·吕萨克定律条件,根据该定律及其推论由体积变化进而求温度的变化.因为管口和大气相通,所以球内气体的体积随温度的升高而膨胀,气体是等压变化,根据盖·吕萨克定律:V1T1=V2T2=ΔVΔT=恒量.温度的增加与体积的增加成正比,所以可以用来测量温度.测量温度的范围应该为气体的体积从V1=100cm3等压变化到V2=100cm3+100×0.2cm3=120cm3,这个范围所对应的气体温度T1~T2之间,根据题意当T0=273K+5K=278K时,气体的体积V0=(100+20×0.2)cm3=104cm3.根据盖·吕萨克定律:V0T0=V1T1所以T1=V1T0V0=100×278104K=267.3KV0T0=V2T2所以T2=V2T0V0=120×278104K=320.8k又267.3K=-5.7℃,320.8K=47.8℃能测量温度的范围是-5.7℃~47.8℃.答案:能;测量温度的范围是-5.7℃~47.8.℃点评:本题易出错在:①错将体积用刻度数乘以0.2cm3,漏掉了空心球的体积.②错把摄氏温度当成热力学温度.③计算时应采用热力学温度.(2010·哈尔滨市模拟)如图所示,A气缸中用活塞封闭有一定质量的理想气体,温度为27℃,活塞与气缸底部距离为h,活塞截面积为S.气缸中的活塞通过滑轮系统挂一重物,质量为m.若不计一切摩擦,当气体的温度升高10℃且系统稳定后,求重物m下降的高度.答案:130h解析:初末状态,物块静止,可知绳中拉力大小相等,分析活塞可知,气体发生等压变化.由盖·吕萨克定律知:V1T1=V2T2=ΔVΔT,V1=Sh,ΔV=SΔhT1=300K,解得Δh=hT1ΔT=130h.图甲所示是一定质量的理想气体由状态A经过状态B变为状态C的V-T图象.已知气体在状态A时的压强是1.5×105Pa.(1)说出A到B过程中压强变化的情形,并根据图象提供的信息,计算图中TA的温度值.(2)请在图乙坐标系中,作出由状态A经过状态B变为状态C的p-T图象,并在图线相应位置上标出字母A、B、C.如果需要计算才能确定有关坐标值,请写出计算过程.解析:(1)由图甲可以看出,A与B的连线的延长线过原点O,所以从A到B是一个等压变化,即pA=pB.根据盖·吕萨克定律可得VA/TA=VB/TB,所以TA=VATBVB=0.4×3000.6K=200K.(2)由图甲可以看出,从B到C是一个等容变化,根据查理定律得pB/TB=pC/TC.所以pC=TCpBTB=400×1.5×105300Pa=2.0×105Pa.则可画出由状态A经B到C的p-T图象如图所示.答案...