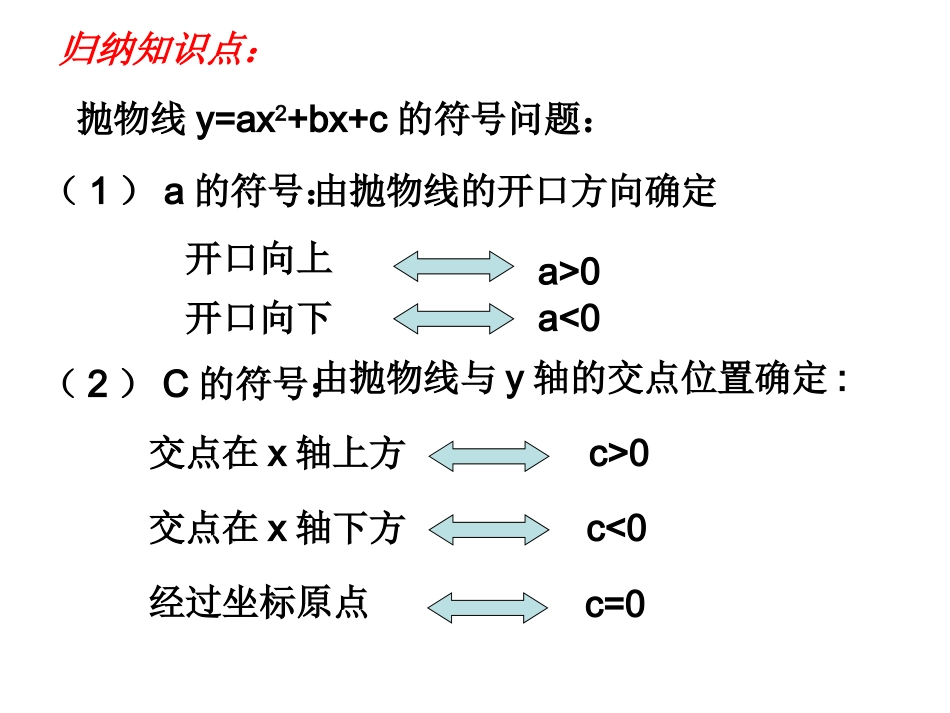
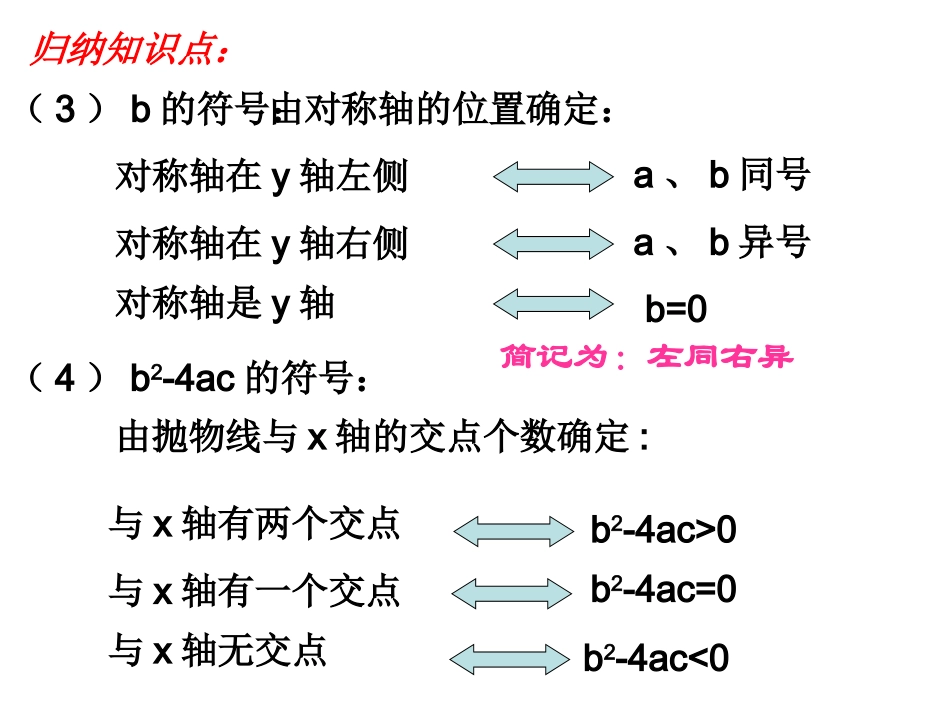
关于二次函数专题图象与字母系数的关系归纳知识点:抛物线y=ax2+bx+c的符号问题:(1)a的符号:由抛物线的开口方向确定开口向上a>0开口向下a<0(2)C的符号:由抛物线与y轴的交点位置确定:交点在x轴上方c>0交点在x轴下方c<0经过坐标原点c=0(3)b的符号:由对称轴的位置确定:对称轴在y轴左侧a、b同号对称轴在y轴右侧a、b异号对称轴是y轴b=0(4)b2-4ac的符号:由抛物线与x轴的交点个数确定:与x轴有两个交点b2-4ac>0与x轴有一个交点b2-4ac=0与x轴无交点b2-4ac<0归纳知识点:简记为:左同右异归纳知识点:抛物线y=ax2+bx+c的符号问题:a+b+c的符号:由x=1时抛物线上的点的位置确定a-b+c的符号:由x=-1时抛物线上的点的位置确定你还可想到啥?(5)抛物线上几个特殊点的坐标所决定的代数式的正负:(1,a+b+c),(-1,a-b+c),(2,4a+2b+c),(-2,4a-2b+c),(6)判断2a+b与2a-b的正负经常由对称轴与±1的关系决定;4a+b与4a-b呢?(7)顶点位置1、原点2、y轴上3、x轴上(8)与x轴的交点A(x1,0);B(x2,0)X1+X2=;AB=归纳知识点:1.已知二次函数y=ax+bx+c²,如果a>0,b<0,c<0,那么这个函数图象的顶点必在()A.第一象限B.第二象限C.第三象限D.第四象限2.如图所示,二次函数y=ax+bx+c²的图象满足()A.a>0,b>0,b2-4ac>0B.a<0,c>0,b2-4ac>0C.a>0,b<0,b2-4ac>0D.a>0,c<0,b2-4ac<0oxy3.已知二次函数y=ax+bx+c²的图象如图所示,则点P(a,bc)在第____象限.oxy4.若一次函数y=ax+b的图象经过第二、三、四象限,则二次函数y=ax2+bx-3的大致图象是()xyoxyoxyoxyoABCD-3-3-3-35.若二次函数y=ax2+bx+c的图象如下,与x轴的一个交点为(1,0),则下列各式中不成立的是()A.b2-4ac>0B.abc>0C.a+b+c=0D.a-b+c<01xyo-16.二次函数y=ax2+bx+c的图象如图,并且对称轴为直线x=1,那么abc,b2-4ac,2a+b,a+b+c这四个代数式中,值为正数的有()A.4个B.3个C.2个D.1个x=17.抛物线y=ax2+bx+c中,b=4a,它的图象如图,有以下结论正确的为():①c<0;②a+b+c>0;③a-b+c>0;④b2-4ac<0;⑤abc<0;⑥4a>c;8、已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:①b>0;②c<0;③4a+2b+c>0;④(a+c)2<b2,其中正确的个数是()A、4个B、3个C、2个D、1个xoyx=1B9.若抛物线y=x-2mx+m+m+1²²的顶点在第二象限,则常数m的取值范围是()A.m<1或m>2B.-1110.同一坐标系中,函数y=mx+m和y=-mx+2x+2(m²是常数,且m≠0)的图象可能是()yxyxyxyxABCDx说出抛物线在下列情况时,系数的特点:(1)、抛物线过一、二、四象限。(2)、抛物线过二、三、四象限。(3)、抛物线不过第二象限。(4)、抛物线不过第四象限。(5)、抛物线过原点及过一、三象限。(6)、抛物线过原点及过二、四象限。cbxaxy2练习: