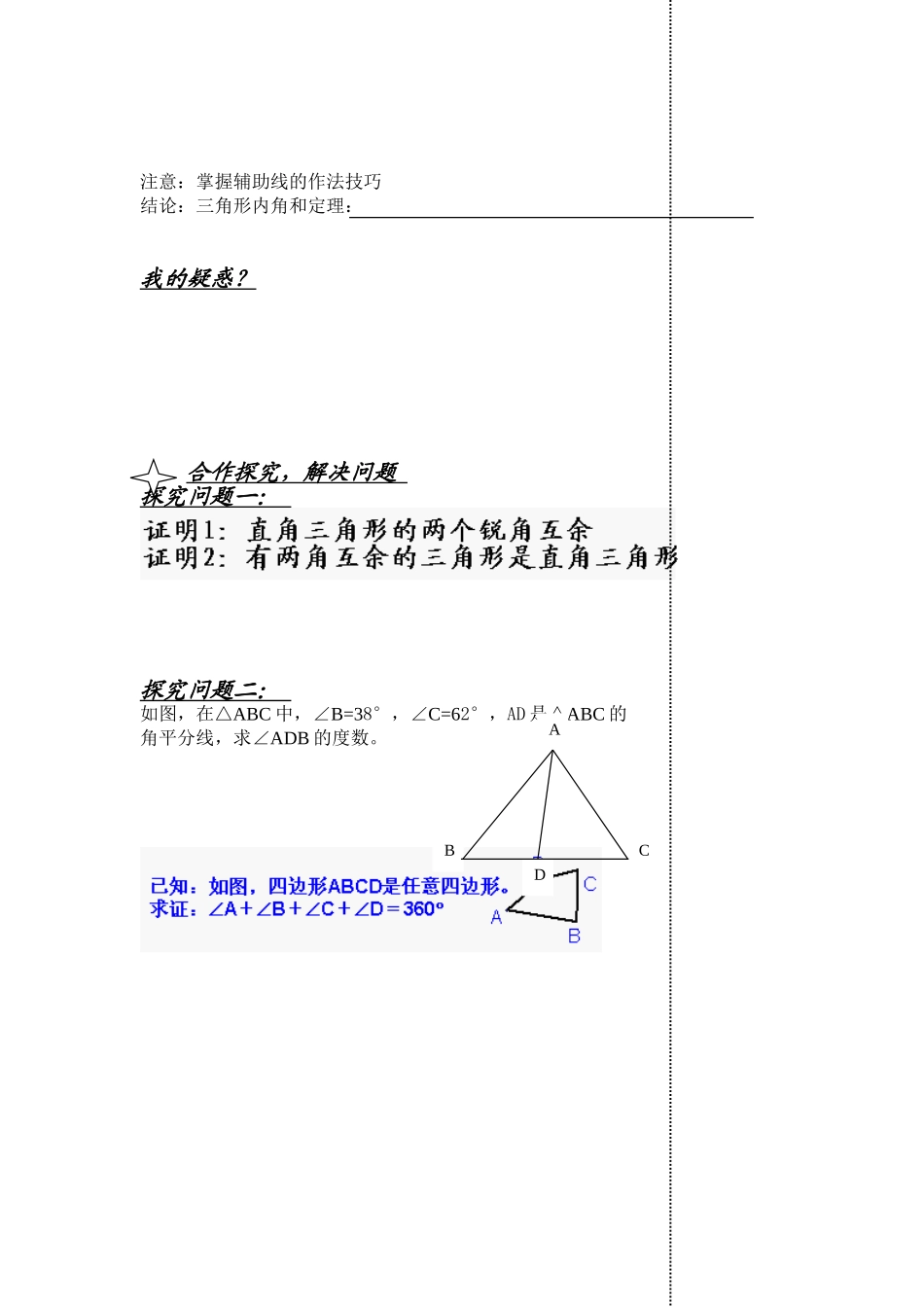
靖边四中导学案第课时----三角形内角和定理(1)学习目标:1.掌握三角形内角和定理的证明及简单应用。2.灵活运用三角形内角和定理解决相关问题。3.用多种方法证明三角形定理,培养一题多解的能力重、难点:重难点:掌握“三角形内角和定理”的证明过程,并能根据这个定理解决实际问题。自主学习,思考问题一.探究新知:阅读教材P178-179活动1:(1)用折纸的方法验证三角形内角和定理.(2)实验1:将纸片三角形三顶角剪下,随意将它们拼凑在一起。(3)用严谨的证明来论证三角形内角和定理.看哪个同学想的方法最多?方法一:过A点作DE∥BC方法二:作BC的延长线CD,过点C作射线CE∥BA.备注动手做一做,相信你能行!ABCDEABCED注意:掌握辅助线的作法技巧结论:三角形内角和定理:我的疑惑?合作探究,解决问题探究问题一:探究问题二:如图,在△ABC中,∠B=38°,∠C=62°,AD是△ABC的角平分线,求∠ADB的度数。CDBA达标检测1、△ABC中可以有3个锐角吗?3个直角呢?2个直角呢?若有1个直角另外两角有什么特点?2、△ABC中,∠C=90°,∠A=30°,∠B=?3、∠A=50°,∠B=∠C,则△ABC中∠B=?4、三角形的三个内角中,只能有____个直角或____个钝角.5、任何一个三角形中,至少有____个锐角;至多有____个锐角.6、三角形中三角之比为1∶2∶3,则三个角各为多少度?7、已知:△ABC中,∠C=∠B=2∠A。(1)求∠B的度数;(2)若BD是AC边上的高,求∠DBC的度数?我的收获(反思静悟、体验成功)