抛物线的参数方程VIP免费

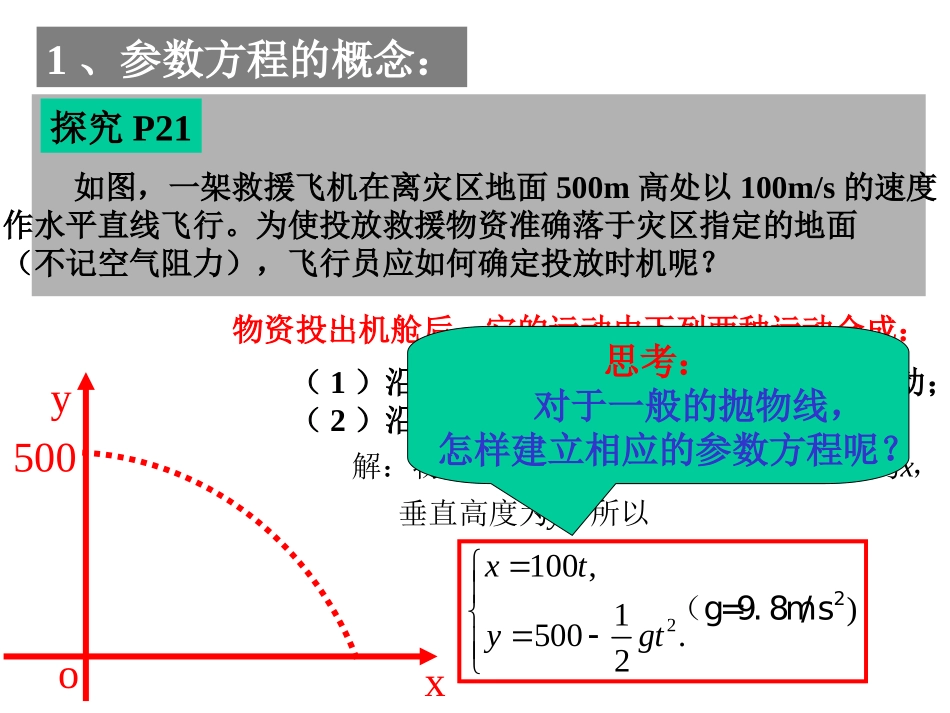
二、圆锥曲线的参数方程1、椭圆的参数方程2、双曲线的参数方程3、抛物线的参数方程1、参数方程的概念：探究P21如图，一架救援飞机在离灾区地面500m高处以100m/s的速度作水平直线飞行。为使投放救援物资准确落于灾区指定的地面（不记空气阻力），飞行员应如何确定投放时机呢？xy500o物资投出机舱后，它的运动由下列两种运动合成：（1）沿ox作初速为100m/x的匀速直线运动；（2）沿oy反方向作自由落体运动。txy解：物资出舱后，设在时刻，水平位移为，垂直高度为，所以2100,)1500.2xtygt2（g=9.8m/s思考：对于一般的抛物线，怎样建立相应的参数方程呢？抛物线的参数方程oyx)HM(x，y)M设（x,y）为抛物线上除顶点外的任意一点，以射线OM为终边的角记作。tan.My因为点（x,y）在的终边上，根据三角函数定义可得x.2又设抛物线普通方程为y=2px,().y22px=tan解出x,y得到抛物线（不包括顶点）的参数方程：为参数2ptan1如果设t=,t(-,0)(0,+),则有tan,().ty2x=2pt为参数2pt0t当时，参数方程表示的点正好就是抛物线的顶点（0，0）。,().ttRy2x=2pt所以，为参数，表示整条抛物线。2pt思考：参数t的几何意义是什么？抛物线的参数方程oyx)HM(x，y)2抛物线y=2px(p>0)的参数方程为:1其中参数t=(0),当=0时，t=0.tan几何意义为：,().ttRy2x=2pt为参数，2pt抛物线上除顶点外的任意一点与原点连线的斜率的倒数。思考：P21怎样根据抛物线的定义选取参数，建立抛物线x2=2py(p>0)的参数方程？.x即P(x,y)为抛物线上任意一点,则有t=y例3、2OABy如图，是直角坐标原点，，是抛物线=2px(p>0)上异于顶点的两动点，且OAOB，OMAB并与AB相交于点M，求点M的轨迹方程。,0.MAB2211221212根据条件，设点，，的坐标分别为（x,y）,(2pt,2pt),(2pt,2pt)(tt且tt）解：OBMAxyOMOAOBAB��211222222121则=（x,y），=(2pt,2pt),=(2pt,2pt)，=(2p(t-t),2p(t-t)).,0,1OAOBOAOB�22121212即(2ptt)+（2p）tt=0,tt。,0,()0OMABOMABxy�222212112即2px(t-t)+2py(t-t)=0,t+t。(0)yxx12即t+t。AMMBAMB�221122因为=（x-2pt,y-2pt），=（2pt-x,2pt-y）,且，，三点共线，221212（x-2pt)(2pt-y）=(y-2pt)(2pt-x)，1212化简，得y(t+t)-2ptt-x=0.1212y将tt=-1，t+t=-代入，得到xyy(-)+2p-x=0,x220(0)ypxxM2即x，这就是点的轨迹方程。探究：P35在例3中，点A，B在什么位置时，三角形AOB的面积最小？最小值是多少？小结作业P364、5