三角形中线的性质VIP免费

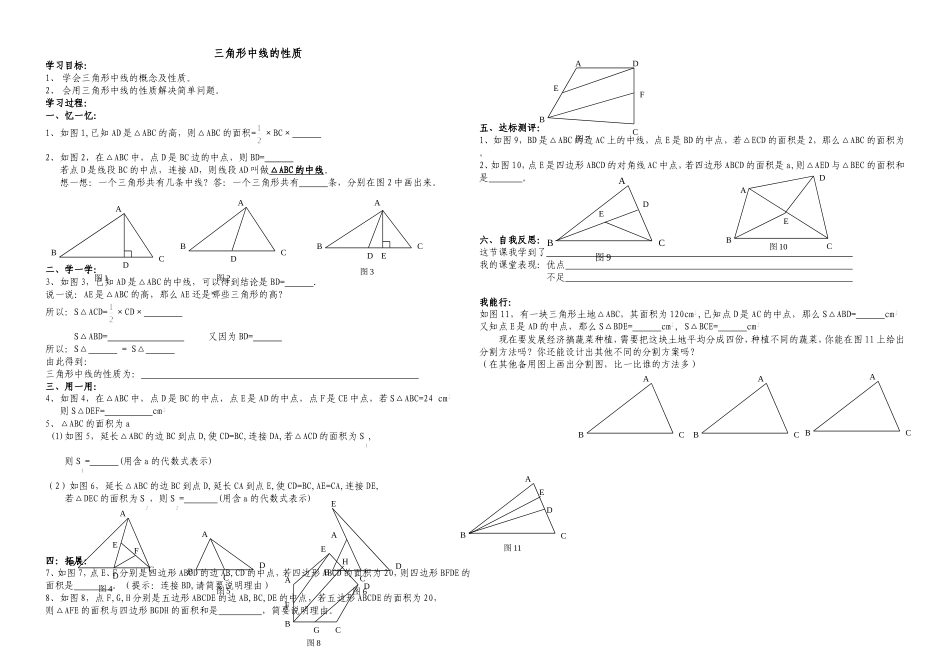
三角形中线的性质学习目标：1、学会三角形中线的概念及性质。2、会用三角形中线的性质解决简单问题。学习过程：一、忆一忆：1、如图1,已知AD是△ABC的高，则△ABC的面积=×BC×2、如图2，在△ABC中，点D是BC边的中点，则BD=若点D是线段BC的中点，连接AD，则线段AD叫做△ABC的中线。想一想：一个三角形共有几条中线？答：一个三角形共有条，分别在图2中画出来。二、学一学：3、如图3，已知AD是△ABC的中线，可以得到结论是BD=.说一说：AE是△ABC的高，那么AE还是哪些三角形的高？所以：S△ACD=×CD×S△ABD=又因为BD=所以：S△=S△由此得到：三角形中线的性质为：三、用一用：4、如图4，在△ABC中，点D是BC的中点，点E是AD的中点，点F是CE中点，若S△ABC=24cm则S△DEF=cm5、△ABC的面积为a(1)如图5，延长△ABC的边BC到点D,使CD=BC,连接DA,若△ACD的面积为S,则S=(用含a的代数式表示)（2）如图6，延长△ABC的边BC到点D,延长CA到点E,使CD=BC,AE=CA,连接DE,若△DEC的面积为S，则S=(用含a的代数式表示)四：拓展：7、如图7，点E、F分别是四边形ABCD的边AB,CD的中点，若四边形ABCD的面积为20，则四边形BFDE的面积是。（提示：连接BD,请简要说明理由）8、如图8，点F,G,H分别是五边形ABCDE的边AB,BC,DE的中点，若五边形ABCDE的面积为20，则△AFE的面积与四边形BGDH的面积和是，简要说明理由。五、达标测评：1、如图9，BD是△ABC的边AC上的中线，点E是BD的中点，若△ECD的面积是2，那么△ABC的面积为。2、如图10，点E是四边形ABCD的对角线AC中点，若四边形ABCD的面积是a,则△AED与△BEC的面积和是。六、自我反思：这节课我学到了我的课堂表现：优点不足我能行：如图11，有一块三角形土地△ABC，其面积为120cm,已知点D是AC的中点，那么S△ABD=cm又知点E是AD的中点，那么S△BDE=cm,S△BCE=cm现在要发展经济搞蔬菜种植，需要把这块土地平均分成四份，种植不同的蔬菜，你能在图11上给出分割方法吗？你还能设计出其他不同的分割方案吗？（在其他备用图上画出分割图，比一比谁的方法多）ABDC图1ABCD图2ABCD图3EABCD图5ABCEDF图4ABCD图6EABCDEF图7AFBGCDHE图8ABCDE图10BACED图11BACBACBACBAC图9ED