二次函数应用1VIP免费

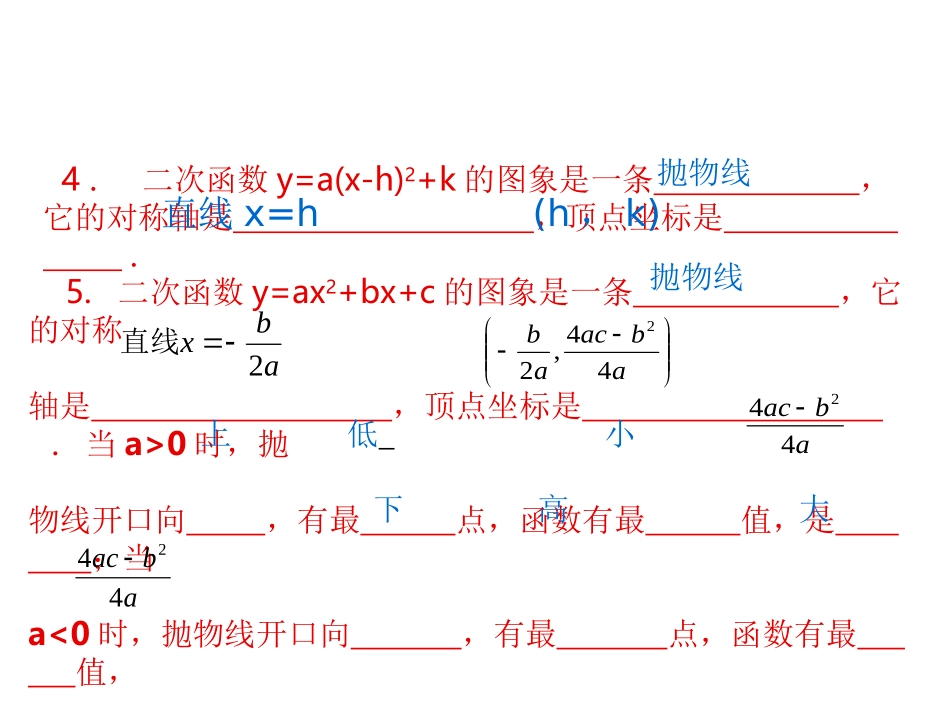
xyoy=ax²+bx+c二次函数的应用1GaoqiaozhongxueMXH2016年9月1.二次函数y=2(x-3)2+5的对称轴是，顶点坐标是。当x=时，y的最值是。2.二次函数y=-3(x+4)2-1的对称轴是，顶点坐标是。当x=时，函数有最值，是。3.二次函数y=2x2-8x+9的对称轴是，顶点坐标是.当x=时，函数有最值，是。直线x=3(3，5)3小5直线x=-4(-4，-1)-4大-1直线x=2(2，1)2小1复习巩固5.二次函数y=ax2+bx+c的图象是一条，它的对称轴是，顶点坐标是.当a>0时，抛物线开口向，有最点，函数有最值，是；当a<0时，抛物线开口向，有最点，函数有最值，是。抛物线abacab44,22abx2直线abac442上小下大abac442高低4.二次函数y=a(x-h)2+k的图象是一条，它的对称轴是，顶点坐标是.抛物线直线x=h(h，k)设矩形的长为x,那么矩形的宽为（20-x)第一节的问题：问题1某水产养殖户用长40m的围网，在水中围成一块矩形的水面，投放鱼苗，要是围成的水面的面积最大，它的长应是多少m?则面积是：S=x(20-x)=-x²+20x①0＜x＜20新课解：S=-x²+20x(0＜x＜20)=-x²+20x-100+100=-(x²-20x+100)+100=-(x-10)²+100∵(0＜x＜20)∴这个函数图像是一条开口向下抛物线的一段，它的顶点坐标是（10，100），所以x=10时s=100∴当x=10时，面积最大=100问题的引申：1：如图，有长为24米的篱笆，一面利用墙（墙的长度足够长）围成长方形养鸡场.设养鸡场的长BC为x米，面积为y平方米，试问：当长方形的长、宽各为多少米时，养鸡场的面积最大，最大面积是多少？ACBD引申2：如图，有长为24米的篱笆，一面利用墙（墙的长度为10米）围成中间隔有一道篱笆的长方形养鸡场.设养鸡场的长BC为x米，面积为y平方米.试问：当长方形的长、宽各为多少米时，养鸡场的面积最大，最大面积是多少？ACBD引申3：如图，有长为24米的篱笆，一面利用墙（墙的长度为10米）围成中间隔有二道篱笆的长方形养鸡场.设养鸡场的长BC为x米，面积为y平方米.试问：当长方形的长、宽各为多少米时，养鸡场的面积最大，最大面积是多少？ACBD问题2某建筑物的窗户如图所示,它的上半部分是半圆,下半部分是矩形,制造窗框的材料总长(图中所有的黑线的长度和)为15m.当x等于多少时,窗户通过的光线最多(结果精确到0.01m)?此时,窗户的面积是多少?何时窗户通过的光线最多?1.4715.yxx【解析】由.4715,xxy得xx21527224715222.222xxxxxxyS窗户面积.562251415272x何时窗户通过的光线最多当x=1.1时，s最大，最大为m2225561、利用二次函数的性质解决生活和生产实际中最大值或最小值问题，它的一般方法是：(1)列出二次函数的解析式，列解析式时，要根据自变量的实际意义，确定自变量的取值范围；(2)在自变量取值范围内，运用公式或配方法求出二次函数的最大值或最小值。2、数学思想方法的运用：（1）数形结合思想；（2）从特殊到一般思想。课后小结20241226年月日12练习与作业•练习：课本p36练习1、2•作业:基础训练第25、26页。