2.1数列的概念和表示课件VIP免费

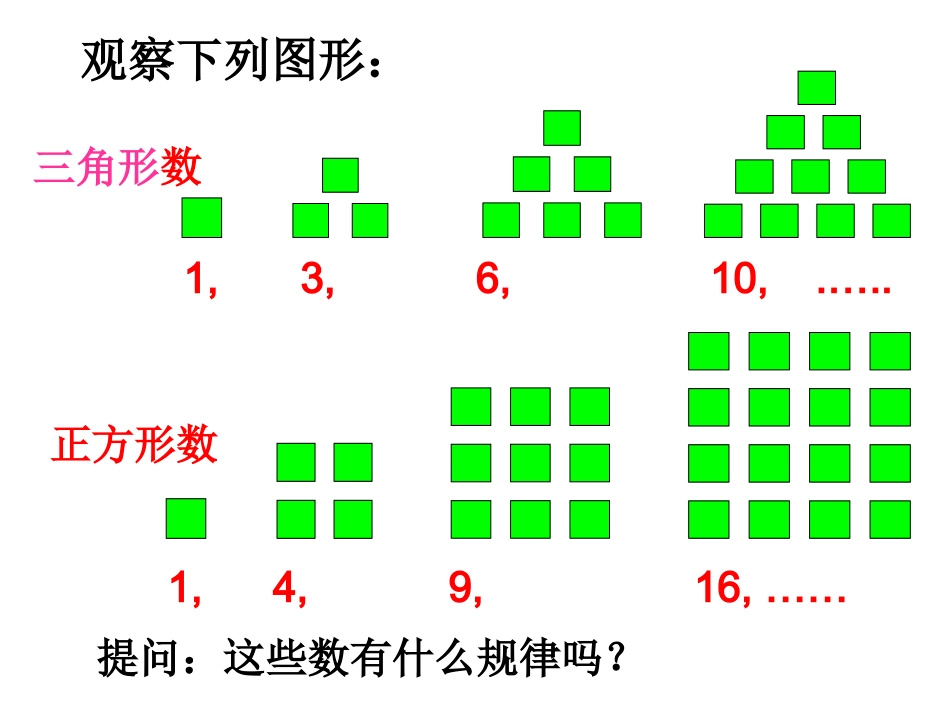
2.1数列的概念与简单表示法三角形数1,3,6,10,.…..正方形数1,4,9,16,……观察下列图形：提问：这些数有什么规律吗？一.定义：一.定义：按照一定顺序排列着的一列数叫数列。按照一定顺序排列着的一列数叫数列。(1)三角形数：1,3,6,10,.…..(2)正方形数：1,4,9,16,……数列中的每一个数叫做这个数列的项。(3)4，5，6，7，8，9，10；(4)10，9，8，7，6，5，4；数列中的每一项都和它的序号有关，排第一位的数称为这个数列的第1项（首项），排第二位的数称为这个数列的第2项，······，排第n位的数称为这个数列的第n项.数列的一般形式可以写成：,,,,,321naaaa其中是数列的第n项，上面的数列又可简记为nana(1)三角形数：1,3,6,10,.…..(2)正方形数：1,4,9,16,……按照一定顺序排列着的一列数叫数列。按照一定顺序排列着的一列数叫数列。(1)三角形数：1,3,6,10,.…..(2)正方形数：1,4,9,16,……一.定义：一.定义：按照一定顺序排列的一列数叫数列。按照一定顺序排列的一列数叫数列。思考1：数列4，5，6，7，8，9，10；数列10，9，8，7，6，5，4；是否相同？思考2：数列中的数是否可以重复？如：数列－1，1，－1，1，···。2）根据数列项的大小分：递增数列：从第2项起，每一项都大于它的前一项的数列。递减数列：从第2项起，每一项都小于它的前一项的数列。常数数列：各项相等的数列。摆动数列：从第2项起，有些项大于它的前一项，有些项小于它的前一项的数列有穷数列：项数有限的数列.例如数列1，2，3，4，5，6。是有穷数列无穷数列：项数无限的数列.例如数列1，2，3，4，5，6，…是无穷数列1）根据数列项数的多少分：二.数列的分类：P28观察观察下列数列的每一项与这一项的序号是否有一定的对应关系？，，，，，51413121112345….项序号2，4，6，8，10，…12345……序号项数列中的每一个数都对应着一个序号，反过来，每个序号也都对应着一个数。三.数列的表示：nn1n2n数列与函数的关系:数列与函数的关系:数列可以看作特殊的函数，序号是其自变量，项是序号所对应的函数值，数列的定义域是正整数集，或是正整数集的有限子集．数列可以看作特殊的函数，序号是其自变量，项是序号所对应的函数值，数列的定义域是正整数集，或是正整数集的有限子集．于是我们研究数列就可借用函数的研究方法，用函数的观点看待数列．于是我们研究数列就可借用函数的研究方法，用函数的观点看待数列．*N*N数列可以看成以正整数集N*（或它的有限子集{1，2，3，4，…,n}）为定义域的函数an=f(n),当自变量按照从小到大的顺序依次取值时，所对应的一列函数值。思考213,123...xyxyx函数与当依次取，，时，其函数值构成怎样的数列？正方形数：1,4,9,16,……通项公式可以看成是数列的函数解析式。{}nann如果数列的第项与之间的关系可以用一个式子来表示，那么这个公式叫做数通序列的号项公式。2nan（1）（2）1nnannann1如果只知道数列的通项公式，那能写出这个数列吗？na根据下面数列的通项公式，写出它的前5项：例1、写出下面数列的一个通项公式，使它的前4项分别是下列各数：。，，，）（；，，，；，，，）（）（020244131211)3(2516942;7,5,3,11练习：P311,3,412nan2)1(nannann1)1(11)1(1nna例2、图中的三角形称为谢宾斯基（Sierpinski）三角形，在下图4个三角形中，着色三角形的个数依次构成一个数列的前4项，请写出这个数列的一个通项公式，并在直角坐标系中画出它的图象。13nnaan30272421181512963o12345n13nna问题：如果一个数列{an}的首项a1=1，从第二项起每一项等于它的前一项的2倍再加1，即an=2an-1+1（nN∈，n>1），（※）你能写出这个数列的前三项吗？递推公式例3设数列满足写出这个数列的前五项。练习：P312{}na11111(1)nnaana递推公式是数列所特有的表示法，它包含两个部分，一是递推关系，一是初始条件，二者缺一不可．递推公式是数列所特有的表示法，它包含两个部分，一是递推关系，一是初始条件，二者缺一不可．.11,22,5,2)6(9999.0,999.0,99.0,9.05555555555549999999999310000100010010)2(.8...