2013-2014学年高中数学人教A版选修2-2同步辅导与检测：1.5.1曲边梯形的面积VIP免费

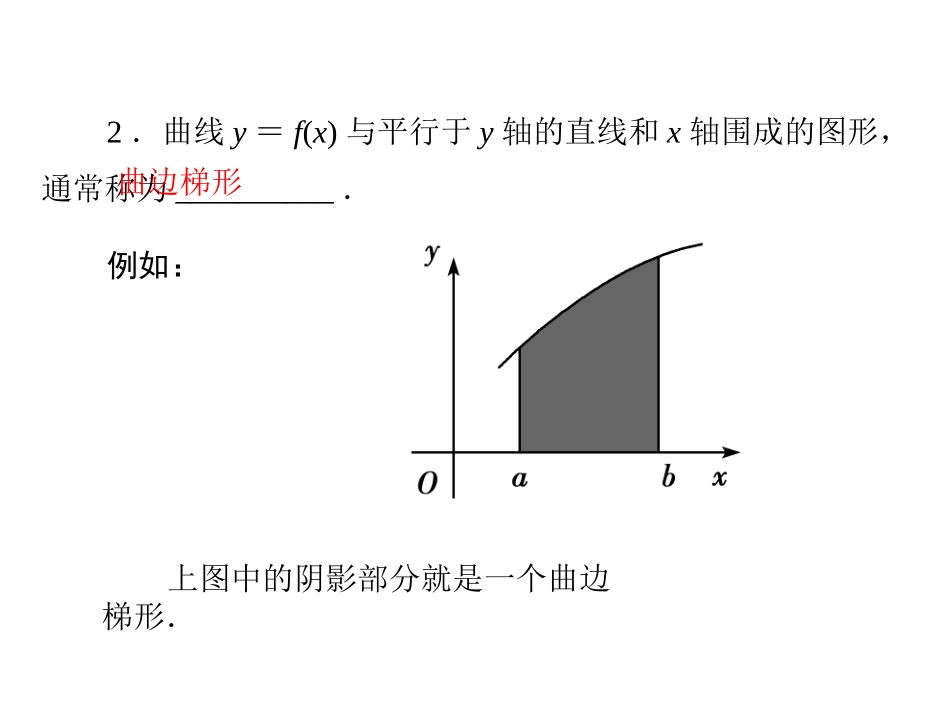
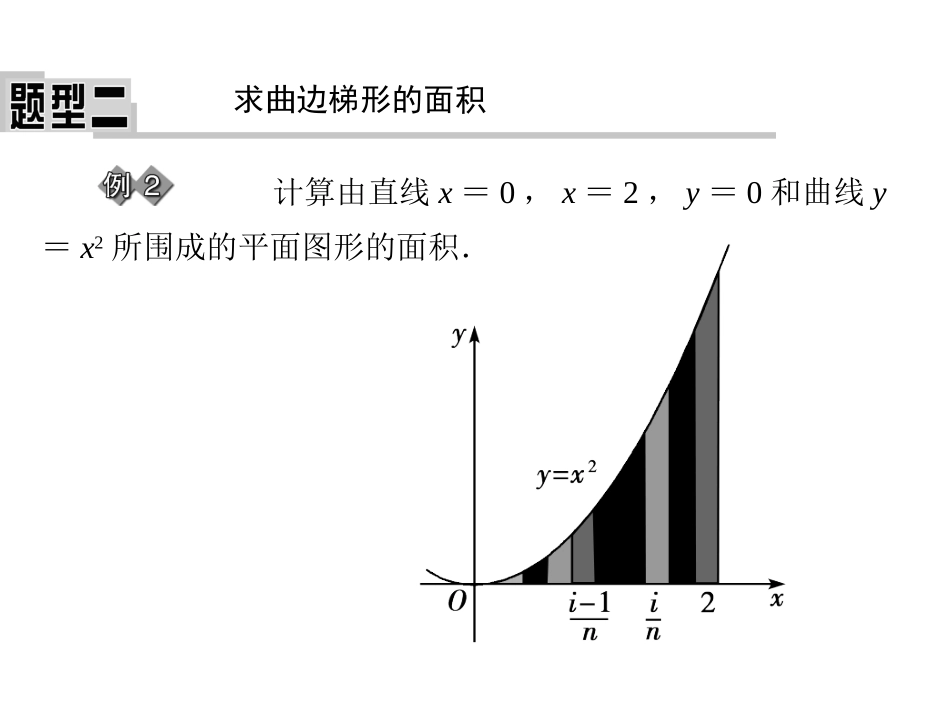
基础梳理1．画出由直线x＝0，x＝2，y＝0和曲线y＝x3所围成的平面图形．答案：所画的图形如右图：2．曲线y＝f(x)与平行于y轴的直线和x轴围成的图形，通常称为__________．例如：曲边梯形上图中的阴影部分就是一个曲边梯形．求曲边梯形的面积计算由直线x＝0，x＝2，y＝0和曲线y＝x2所围成的平面图形的面积．解析：(1)分割．在区间[0,2]上等间隔地插入n－1个点，将它等分成n个小区间：，…，.其长度为Δx＝.分别过上述n－1个分点作x轴的垂线，把曲边梯形分成n个小曲边梯形，它们的面积分别记作ΔS1，ΔS2，…，ΔSn.显然，S＝(2)近似代替．记f(x)＝x2.当n很大，即Δx很小时，在区间上，可以认为函数f(x)＝x2的值变化很小，近似地等于一个常数，不妨认为它近似地等于左端点处的函数值f.这样，在区间上，用小矩形的面积ΔS′i近似代替ΔSi，即在局部小范围内“以直代曲”，则有ΔSi≈ΔS′i＝f·Δx＝(i＝1,2，…，n)．1．连续函数f(x)在[a，b]上的定积分，记作________，即________________________________．例如：函数f(x)＝x2在[0,1]上的定积分，记作__________，即___________________________．2．函数f(x)在[a，b]上的定积分f(x)dx，区间[a，b]叫做____________，函数f(x)叫做____________．基础梳理baf(x)dxbabax2dx1010积分区间被积函数金品质高追求我们让你更放心！•◆◆数学选修•数学选修•2-2(•2-2(•配人教配人教AA版版))◆◆3．定积分f(x)dx(f(x)＞0)的几何意义是什么？例如：定积分x3dx的几何意义是__________________________________________________________________．4．直线x＝0,x＝π，y＝0与曲线y＝sinx所围成的图形的面积用积分表示为________．ba20答案：几何意义是：由直线x＝a，x＝b，y＝0和曲线y＝f(x)所围成的曲边梯形的面积．由直线x＝0，x＝2，y＝0和曲线y＝x3所围成的曲边梯形的面积sinxdx0金品质高追求我们让你更放心！•◆◆数学选修•数学选修•2-2(•2-2(•配人教配人教AA版版))◆◆5．用定积分表示下图中阴影部分的面积．S＝f1(x)dx－f2(x)dxbaba答案：6．定积分x3dx的取值的符号为________，x3dx的取值的符号为______，x3dx的取值的符号为________．100111正负0金品质高追求我们让你更放心！•◆◆数学选修•数学选修•2-2(•2-2(•配人教配人教AA版版))◆◆自测自评1．定积分dx的值等于()A．1B．2C．3D．420解析：定积分dx等于直线y＝与x＝0，x＝2，y＝0围成的三角形的面积，S＝×2×1＝1.答案：A2012金品质高追求我们让你更放心！•◆◆数学选修•数学选修•2-2(•2-2(•配人教配人教AA版版))◆◆3．计算dx＝()A．8πB．16πC．4πD．32π40解析：dx表示以原点为圆心，4为半径的圆的面积，∴dx＝π·42＝4π.答案：C40144014金品质高追求我们让你更放心！•◆◆数学选修•数学选修•2-2(•2-2(•配人教配人教AA版版))◆◆用几何意义求定积分用定积分的意义求下列各式的值：(1)(3x＋1)dx；(2)－dx.313232金品质高追求我们让你更放心！•◆◆数学选修•数学选修•2-2(•2-2(•配人教配人教AA版版))◆◆解析：(1)由直线x＝－1，x＝3，y＝0以及y＝3x＋1所围成的图形，如图所示．(3x＋1)dx表示由直线x＝－1，x＝3，y＝0以及y＝3x＋1所围成的图形在x轴上方的面积减去在x轴下方的面积，3131金品质高追求我们让你更放心！•◆◆数学选修•数学选修•2-2(•2-2(•配人教配人教AA版版))◆◆跟踪训练2．根据定积分的几何意义推出下列定积分的值：(1)xdx；(2)cosxdx；(3)|x|dx.112011解析：(1)如图①，xdx＝(－A1＋A1)＝0.(2)如图②，cosxdx＝A1－A2＋A3＝0.1120金品质高追求我们让你更放心！•◆◆数学选修•数学选修•2-2(•2-2(•配人教配人教AA版版))◆◆(3)如图③， A1＝A2，∴|x|dx＝2A1＝2×＝1.(A1，A2，A3分别表示图中相应各处的面积)1112金品质高追求我们让你更放心！•◆◆数学选修•数学选修•2-2(•2-2(•配人教配人教AA版版))◆◆解析：由定积分的性质：f(x)dx＝f(x)dx＋f(x)dx，得f(x)dx＝f(x)dx－f(x)dx＝0－1＝－1.答案：－122022002...