高中数学 第四章 已知三角函数值求角（2）教案VIP免费

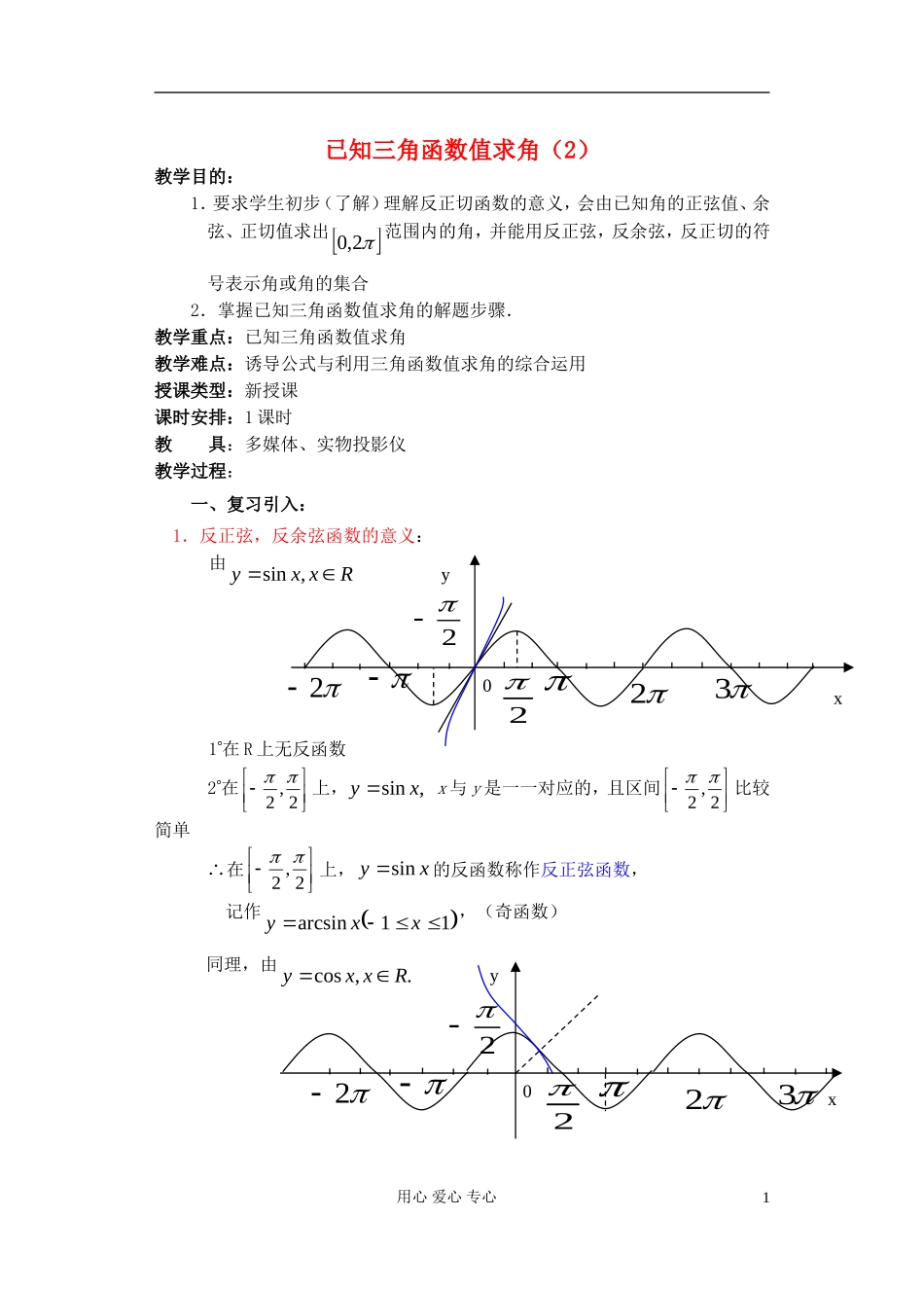
已知三角函数值求角（2）教学目的：1．要求学生初步（了解）理解反正切函数的意义，会由已知角的正弦值、余弦、正切值求出2,0范围内的角，并能用反正弦，反余弦，反正切的符号表示角或角的集合2．掌握已知三角函数值求角的解题步骤．教学重点：已知三角函数值求角教学难点：诱导公式与利用三角函数值求角的综合运用授课类型：新授课课时安排：1课时教具：多媒体、实物投影仪教学过程：一、复习引入：1．反正弦，反余弦函数的意义：由Rxxy,sin1在R上无反函数2在2,2上，,sinxyx与y是一一对应的，且区间2,2比较简单在2,2上，xysin的反函数称作反正弦函数，记作11arcsinxxy，（奇函数）同理，由.,cosRxxy用心爱心专心132222xy032222xy0在,0上，xycos的反函数称作反余弦函数，记作11arccosxxy2．已知三角函数求角：求角的多值性法则：1、先决定角的象限2、如果函数值是正值，则先求出对应的锐角x；如果函数值是负值，则先求出与其绝对值对应的锐角x，3、由诱导公式，求出符合条件的其它象限的角二、讲解新课：反正切函数Rxkxxy,2,tan1在整个定义域上无反函数2在2,2上xytan的反函数称作反正切函数，记作Rxxyarctan（奇函数）三、讲解范例：例1（1）已知2,231tanxx且，求x（精确到1.0）解：在区间2,2上xytan是增函数，符合条件的角是唯一的10'26180x（2）已知31tanx且2,0x，求x的取值集合解：1010,10tan10tanxx或所求的x的集合是1011,10（即31arctan31arctanxx和）用心爱心专心2x0y（3）已知Rxx且31tan，求x的取值集合解：由上题可知：10kx，zkkx1011合并为zkkx10例2已知23sin，根据所给范围求：1为锐角2为某三角形内角3为第二象限角4R解：1由题设32设31，或32323zkk3224由题设zkkkkk3123arcsin1例3求适合下列关系的x的集合1Rxx2cos2201tan32x353sinx解：1zkkkxx,4222arccos2,22cos所求集合为zkkxx,42|2,6,33tankxx所求集合为zkkxx,6|353arcsin1,53sinkkxx例4直角ABC锐角A，B满足：AAAB求,1sintan2cos22解：由已知：1sintancos1AAB用心爱心专心3AAA,tansin2为锐角，0sinA3,20,21cosAAA例51用反三角函数表示)23,(,65sinxx中的角x2用反三角函数表示)27,3(,5tanxx中的角x解：1 23x∴02x又由65sinx得65)sin(x∴)65arcsin(x∴)65arcsin(x2 273x∴230x又由5tanx得5)3tan(x∴5arctan3x∴5arctan3x例6已知21)32cos(x，求角x的集合解： 21)32cos(x∴)(32232Zkkx由32232kx得)(324Zkkx由32232kx得)(24Zkkx故角x的集合为},24324|{Zkkxkxx或例7求3arctan2arctan1arctan的值解：arctan2=,arctan3=则tan=2，tan=3且24，24∴132132tantan1tantan)tan(用心爱心专心4而2∴+=43又arctan1=4∴3arctan2arctan1arctan=例8求y=arccos(sinx),(323x)的值域解：设u=sinx 323x∴123u∴65)arccos(sin0x∴所求函数的值域为]65,0[四、课堂练习：1若cosx＝0，则角x等于()A．ｋπ，（ｋ∈Z）Ｂ．2＋ｋπ，（ｋ∈Z）Ｃ．2＋2ｋπ，（ｋ∈Z）Ｄ．－2＋2ｋ...