高中数学 第一章 立体几何初步 1.2 点、线、面之间的位置关系 1.2.3 直线与平面的位置关系教案3 苏教版必修2-苏教版高一必修2数学教案VIP免费

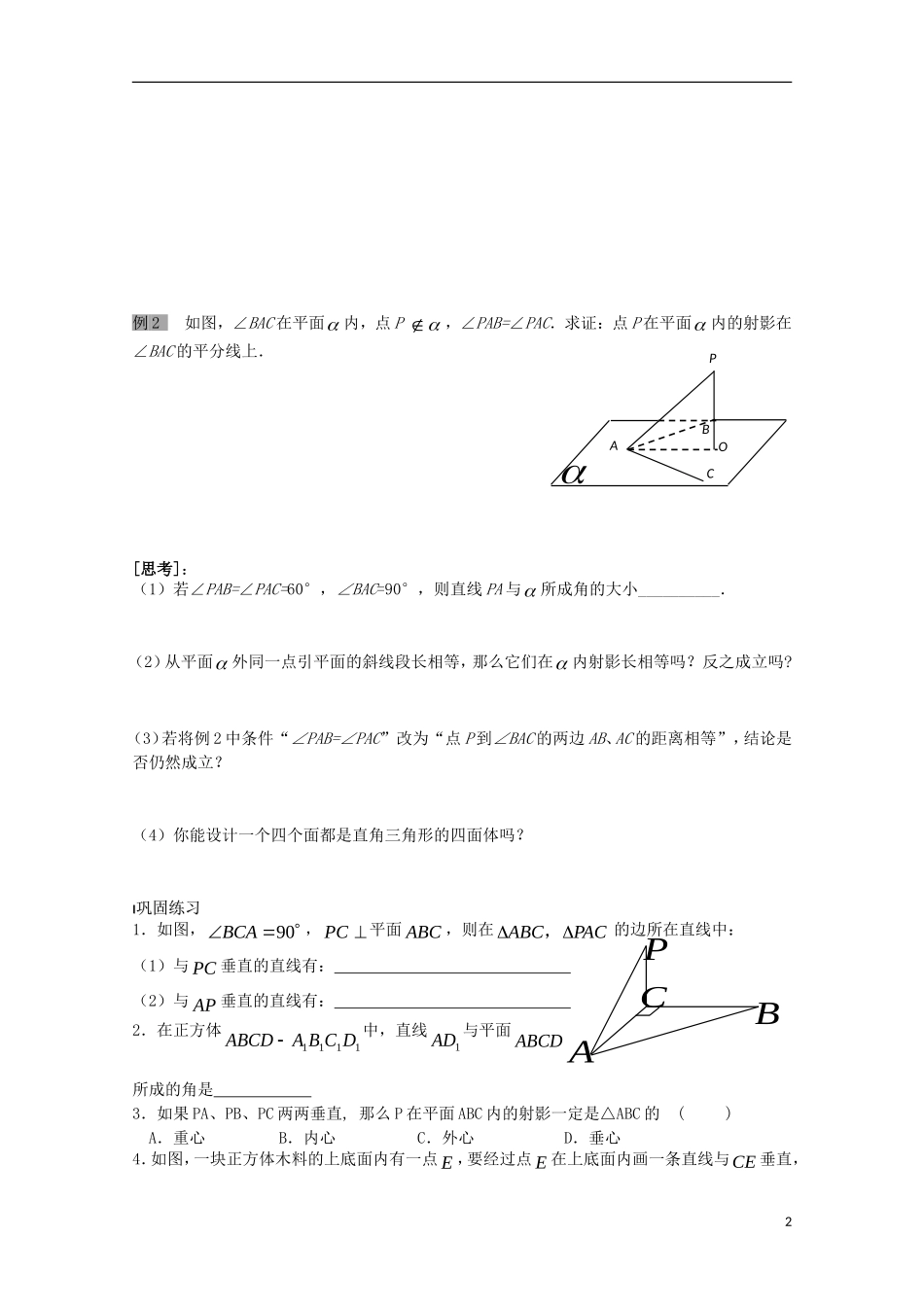
1.2点、线、面之间的位置关系1.2.3直线与平面的位置关系教学目标了解直线和平面所成角的概念和范围；能熟练地运用直线和平面垂直的判定定理和性质定理.重点难点直线与平面所成角的概念．引入新课引入新课1．通过观察一条直线与一个平面相交，思考如何量化它们相交程度的不同．2．平面的斜线的定义：；叫做斜足；叫做这个点到平面的斜线段．3．过平面外一点P向平面引斜线和垂线，那么过斜足Q与垂足1P的直线就是；线段QP1就是线段PQ．4．斜线与平面所成的角的概念，其范围是．指出右上图中斜线PQ与平面所成的角是，你能证明这个角是PQ与平面内经过点Q的直线所成的所有角中最小的角吗？一条直线垂直于平面时，这条直线与平面所成的角是；一条直线与平面平行或在平面内，我们说他们所成的角是．思考：直线与平面所成的角的范围是．例题剖析例题剖析例1如图：已知AC，AB分别是平面垂线和斜线，BC，分别是垂足和斜足，a，aBC，求证：aAB．能用文字语言表述这个结论吗？1PQ1PABCa例2如图，∠BAC在平面内，点P，∠PAB=∠PAC．求证：点P在平面内的射影在∠BAC的平分线上．[思考]：（1）若∠PAB=∠PAC=60°，∠BAC=90°，则直线PA与所成角的大小__________．（2）从平面外同一点引平面的斜线段长相等，那么它们在内射影长相等吗？反之成立吗?（3）若将例2中条件“∠PAB=∠PAC”改为“点P到∠BAC的两边AB、AC的距离相等”，结论是否仍然成立？（4）你能设计一个四个面都是直角三角形的四面体吗？巩固练习巩固练习1．如图，90BCA，PC平面ABC，则在PACABC，的边所在直线中：（1）与PC垂直的直线有：（2）与AP垂直的直线有：2．在正方体1111DCBAABCD中，直线1AD与平面ABCD所成的角是3．如果PA、PB、PC两两垂直,那么P在平面ABC内的射影一定是△ABC的()A．重心B．内心C．外心D．垂心4．如图，一块正方体木料的上底面内有一点E，要经过点E在上底面内画一条直线与CE垂直，2APOCBPBCA应怎样画？课堂小结课堂小结平面的斜线及斜线在平面内的射影的概念；直线与平面所成的角概念、范围．3EC课后训练课后训练一基础题1．若直线a与平面不垂直，那么在平面内与直线a垂直的直线（）.A只有一条.B有无数条.C是平面内的所有直线.D不存在2．设PA、PB、PC是从点P引出的三条射线,每两条的夹角都等于60°，则直线PC与平面APB所成角的余弦值是．3．在三棱锥P-ABC中，顶点P在平面ABC内的射影是△ABC的外心，则三条侧棱PA、PB、PC大小关系是_________________．二提高题4．在四棱锥ABCDP中，ABCD是矩形，PA平面ABCD．（1）指出图中有哪些三角形是直角三角形，并说明理由；（2）若ABADPA，试求PC与平面ABCD所成角的正切值．5．求证：如果平面内的一条直线与这个平面的一条斜线垂直，那么这条直线就和这条斜线在这个平面内的射影垂直．三能力题6．在三棱锥P－ABC中，点P在平面ABC上的射影O是△ABC的垂心，求证：PA⊥BC．4AOPCBABDCP