高中数学 第一章 立体几何初步 1.2 点、线、面之间的位置关系 1.2.3 直线与平面的位置关系教案2 苏教版必修2-苏教版高一必修2数学教案VIP免费

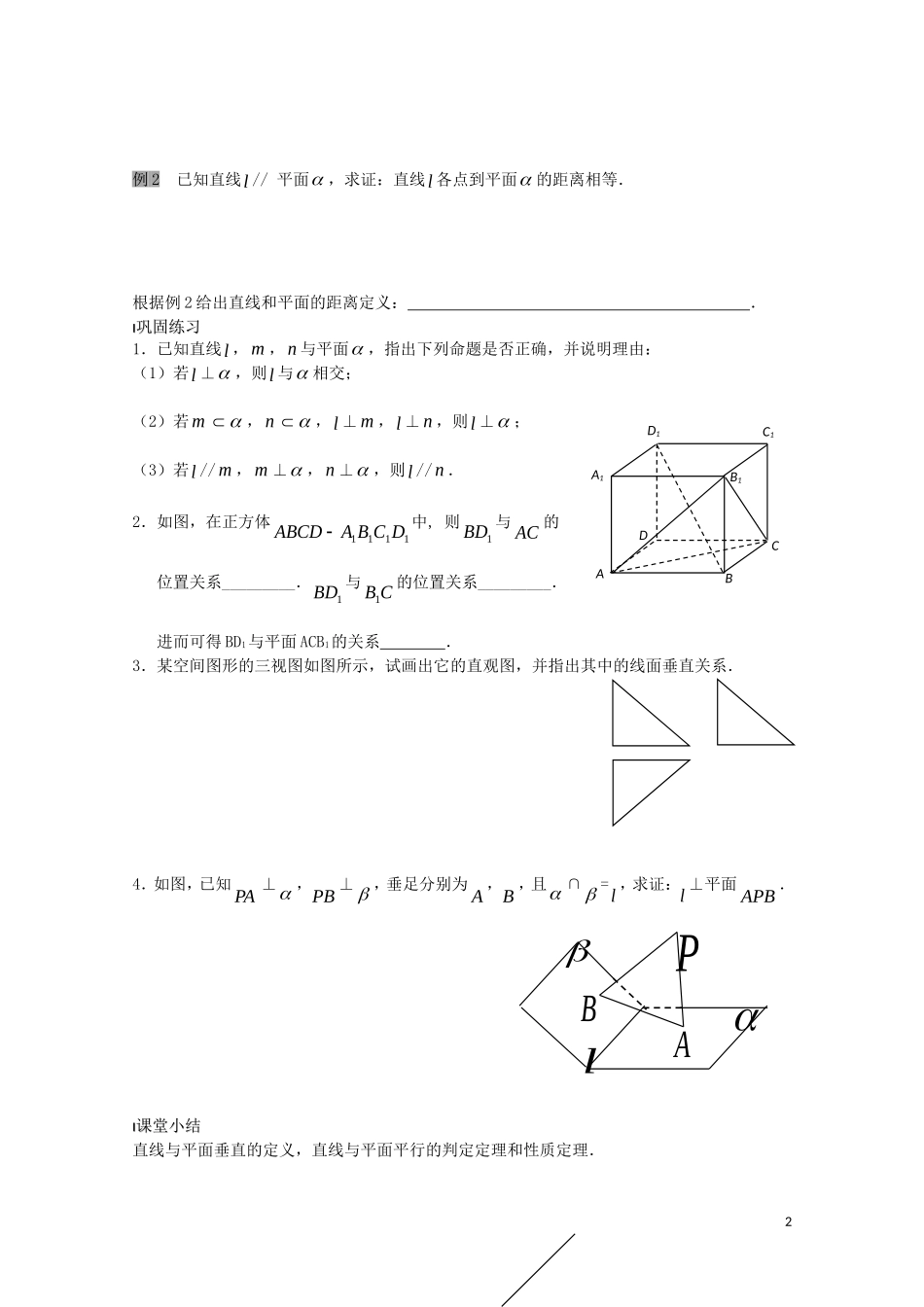
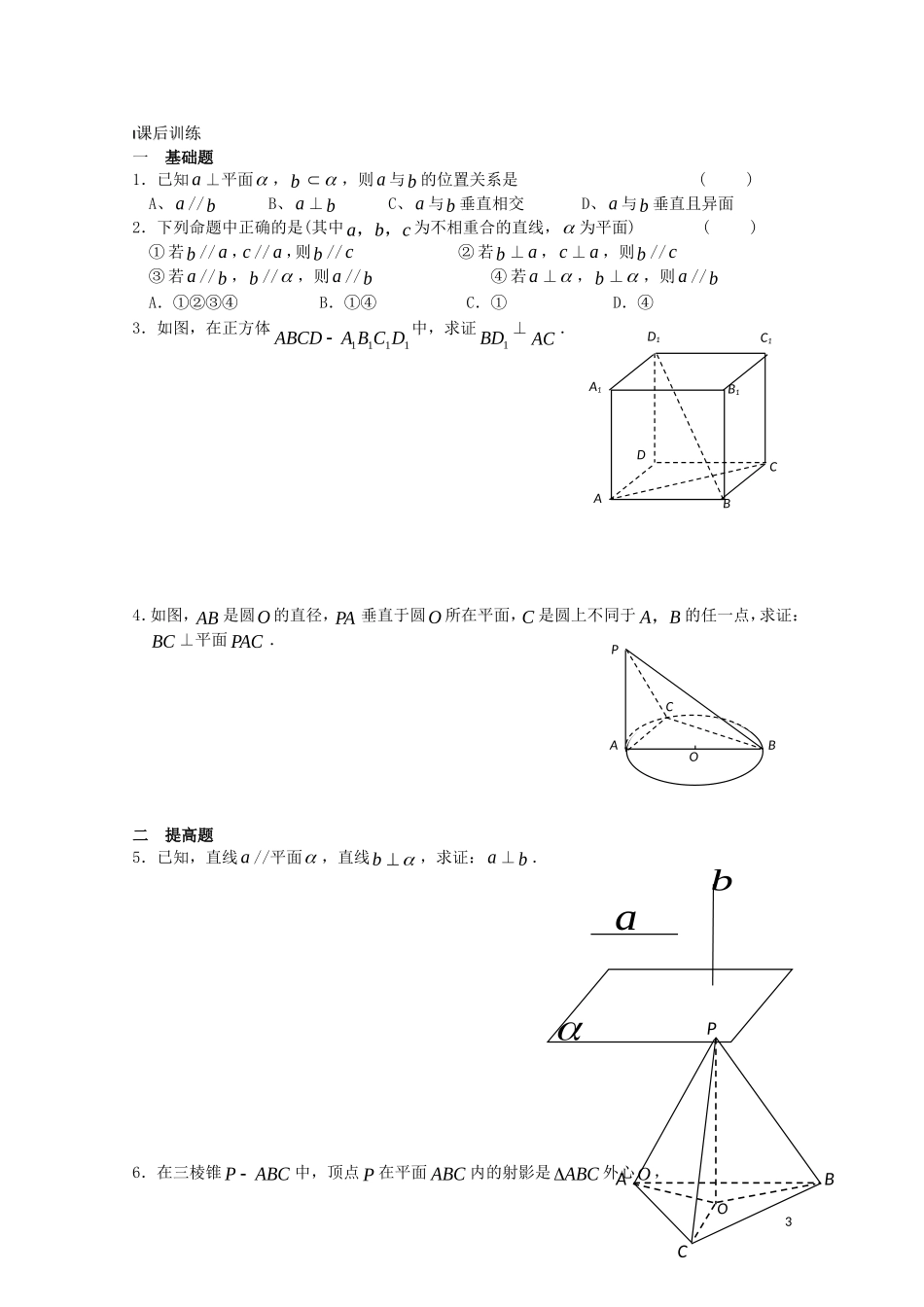
1.2点、线、面之间的位置关系1.2.3直线与平面的位置关系教学目标理解直线和平面垂直的定义及相关概念；掌握直线和平面垂直的判定定理和性质定理；能初步应用这两个定理．重点难点直线与平面垂直的定义和判定定理的探究．引入新课引入新课1．观察：①圆锥的轴与底面半径都垂直吗？为什么？②圆锥的轴与底面所有直线都垂直吗？为什么？③圆锥的轴与底面垂直吗？2．直线与平面垂直的定义：如果一条直线a与一个平面内的直线都，那么直线a与平面互相垂直，记作．直线a叫做平面；平面叫做直线a的；垂线和平面的交点称为．思考：①正投影的投影线与投影面垂直吗？斜投影呢？②在空间过一点有几条直线与已知平面垂直？③在空间过一点有几个平面与已知直线垂直？3．从平面外一点引平面的垂线，，叫做这个点到这个平面的距离．4．直线和平面垂直的判定定理语言表示：符号表示：4．直线和平面垂直的性质定理语言表示：符号表示：例题剖析例题剖析例1求证：如果两条平行直线中的一条垂直于一个平面，那么另一条直线也垂直于这个平面．1图形表示：图形表示：例2已知直线l//平面，求证：直线l各点到平面的距离相等．根据例2给出直线和平面的距离定义：．巩固练习巩固练习1．已知直线l，m，n与平面，指出下列命题是否正确，并说明理由：（1）若l⊥，则l与相交；（2）若m，n，l⊥m，l⊥n，则l⊥；（3）若l//m，m⊥，n⊥，则l//n．2．如图，在正方体1111DCBAABCD中,则1BD与AC的位置关系_________．1BD与CB1的位置关系_________．进而可得BD1与平面ACB1的关系．3．某空间图形的三视图如图所示，试画出它的直观图，并指出其中的线面垂直关系．4．如图，已知PA⊥，PB⊥，垂足分别为A，B，且∩=l，求证：l⊥平面APB．课堂小结课堂小结直线与平面垂直的定义，直线与平面平行的判定定理和性质定理．2lABPABCDD1A1C1B1课后训练课后训练一基础题1．已知a⊥平面，b，则a与b的位置关系是()A、a//bB、a⊥bC、a与b垂直相交D、a与b垂直且异面2．下列命题中正确的是(其中cba，，为不相重合的直线，为平面)()①若b//a，c//a，则b//c②若b⊥a，c⊥a，则b//c③若a//b，b//，则a//b④若a⊥，b⊥，则a//bA．①②③④B．①④C．①D．④3．如图，在正方体1111DCBAABCD中，求证1BD⊥AC．4．如图，AB是圆O的直径，PA垂直于圆O所在平面，C是圆上不同于BA，的任一点，求证：BC⊥平面PAC．二提高题5．已知，直线a//平面，直线b，求证：a⊥b．6．在三棱锥ABCP中，顶点P在平面ABC内的射影是ABC外心O，3abOABPCABCDD1A1C1B1AOPCB求证：PCPBPA．三能力题7．证明：过一点和已知平面垂直的直线只有一条．4