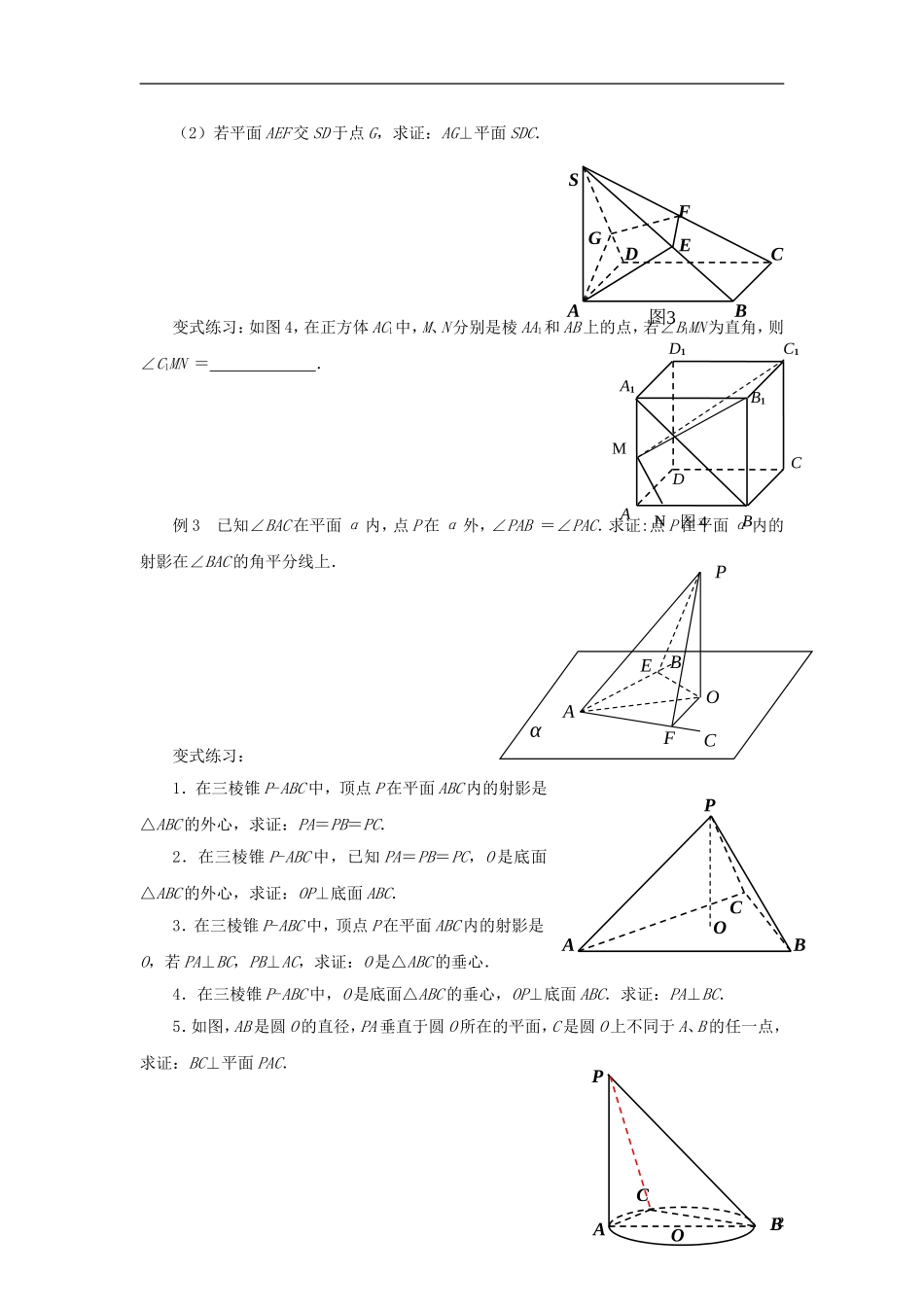
1.2.3直线与平面的位置关系(4)教学目标:1.系统理解掌握直线与平面的平行、垂直的判定和性质的应用;2.会比较熟练地运用有关结论完成证明;3.培养学生的几何直观能力,提高学生的归纳概括能力.教学重点:直线与平面的平行、垂直的判定.教学难点:线面平行、垂直的性质与判定的综合应用.教学方法:合作交流,启发式.教学过程:一、问题情境1.复习:(1)线面平行的定义、判定、性质;(2)线面垂直的定义、判定、性质;2.情境练习:(1)在空间中,下列命题:①平行于同一条直线的两条直线互相平行;②垂直于同一条直线的两条直线互相平行;③平行于同一个平面的两条直线互相平行;④垂直于同一个平面的两条直线互相平行.其中正确的是.(2)如图1,PA⊥平面ABC,在△ABC中,BC⊥AC,则图中直角三角形有个二、典型例题例1如图2,在四棱锥P-ABCD中,M,N分别是AB,PC的中点,若ABCD是平行四边形,求证:MN∥平面PAD.例2已知矩形ABCD中,过A点作SA⊥平面ABCD,再过点A作AE⊥SB于点E,过点E作EF⊥SC于点F,(1)求证:AF⊥SC;1PABC图1PABCDMN图2(2)若平面AEF交SD于点G,求证:AG⊥平面SDC.变式练习:如图4,在正方体AC1中,M、N分别是棱AA1和AB上的点,若∠B1MN为直角,则∠C1MN=.例3已知∠BAC在平面α内,点P在α外,∠PAB=∠PAC.求证:点P在平面α内的射影在∠BAC的角平分线上.变式练习:1.在三棱锥P-ABC中,顶点P在平面ABC内的射影是△ABC的外心,求证:PA=PB=PC.2.在三棱锥P-ABC中,已知PA=PB=PC,O是底面△ABC的外心,求证:OP⊥底面ABC.3.在三棱锥P-ABC中,顶点P在平面ABC内的射影是O,若PA⊥BC,PB⊥AC,求证:O是△ABC的垂心.4.在三棱锥P-ABC中,O是底面△ABC的垂心,OP⊥底面ABC.求证:PA⊥BC.5.如图,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆O上不同于A、B的任一点,求证:BC⊥平面PAC.2αABCPOEFABCDSEFG图3PACBOABCPOMA1C1B1D1ABCD图4N三、要点归纳与方法小结1.线线平行线面平行;2.线线垂直线面垂直线线垂直;3.数学方法:转化、类比.3