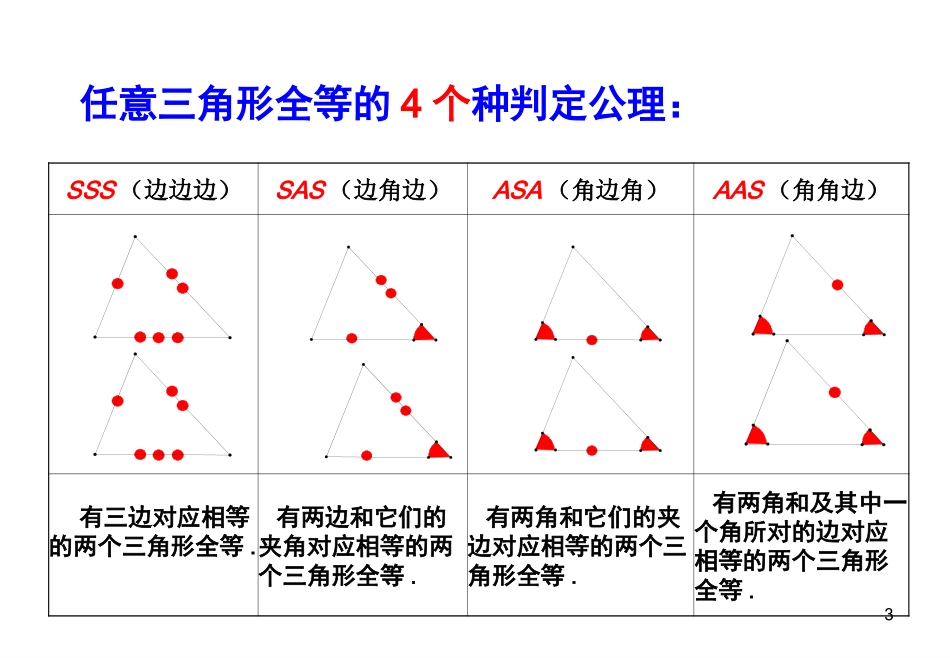
《数学》(北师大.七年级下册)一、全等三角形概念:能够的三角形是全等三角形.二、全等三角形性质:全等三角形对应边.全等三角形对应角.3、全等三角形的判定:(1)一般三角形全等的判定:SSS,SAS,ASA,AAS(2)直角三角形全等的判定:除以上方法外,还有HL注意:1、“分别对应相等”是关键2、两边及其中一边的对角分别对应相等的两个三角形不一定全等3任意三角形全等的4个种判定公理:SSS(边边边)SAS(边角边)ASA(角边角)AAS(角角边)有三边对应相等的两个三角形全等.有两边和它们的夹角对应相等的两个三角形全等.有两角和它们的夹边对应相等的两个三角形全等.有两角和及其中一个角所对的边对应相等的两个三角形全等.两边和其中一边的对角对应相等的两个三角形不一定全等。\=\=SSA5三个角对应相等的两个三角形不一定全等AAA一、全等三角形性质应用1:如图,△AOB≌△COD,AB=7,∠C=60°则CD=,∠A=.ABCDO一、全等三角形性质应用2:已知△ABC≌△DEF,∠A=60°,∠C=50°则∠E=.CBAFED一、全等三角形性质应用3:如图,△ABCDEF≌△,DE=4,AE=1,则BE的长是()A.5B.4C.3D.2FEDCBA1、如图所示,:已知AC=AD,请你添加一个条件————,使得△ABC≌△ABDBACD思路思路已知两边找另一边(SSS)找夹角(SAS)隐含条件AB=AB二、全等三角形判定变式1:如图,已知∠C=D∠,请你添加一个条件————,使得△ABC≌△ABDBACD思路思路已知一边一角这边为角的对边找任一角(AAS)隐含条件AB=AB变式2:如图,已知∠CAB=DAB∠,请你添加一个条件————,使得△ABC≌△ABDBACD思路思路已知一边一角这边为角的邻边夹角的另一边(SAS)夹边的另一角(ASA)找边的另一角(AAS)隐含条件AB=AB如图,已知∠B=E∠,要识别△ABCAED≌△,需要添加的一个条件是--------------思路已知两角:找夹边找一角的对边ABCDEAB=AEAC=AD或DE=BC(ASA)(AAS)课堂练习课堂练习::已知已知::如图如图∠∠B=DEF,BC=EF∠B=DEF,BC=EF∠,,补充条件补充条件求证求证::ΔABCΔABC≌≌ΔDEFΔDEF∠∠ACB=DEF∠ACB=DEF∠AB=DEAB=DEAB=DEAB=DE、、AC=DFAC=DFAABBCCDDEEFF====DDEEFFAABBCC∠∠A=D∠A=D∠(1)(1)若要以“若要以“SAS”SAS”为依据,还缺条件_____为依据,还缺条件_____;;(2)(2)若要以“若要以“ASA”ASA”为依据,还缺条件____;为依据,还缺条件____;(4)(4)若要以“若要以“SSS”SSS”为依据,还缺条件_____;为依据,还缺条件_____;(3)(3)若要以“若要以“AAS”AAS”为依据,还缺条件_____为依据,还缺条件_____;;(5)(5)若若∠∠B=DEF=90°∠B=DEF=90°∠要以“要以“HLHL””为依据,为依据,还缺条件_____还缺条件_____AC=DF二小试牛刀1.如图,在△ABC和△BAD中,BC=AD,请你再补充一个条件,使△ABC≌△BAD.你补充的条件是.DABC二、小试牛刀ABCEF2.已知:如图,△AEF与△ABC中,∠E=B,∠EF=BC.请你添加一个条件,使△AEFABC.≌△小试牛刀例2、如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是拿()去配.17三、熟练转化“间接条件”判全等6如图,AE=CF,∠AFD=CEB∠,DF=BE,△AFD与△CEB全等吗?为什么?ADBCFE8.“三月三,放风筝”如图(6)是小东同学自己做的风筝,他根据AB=AD,BC=DC,不用度量,就知道∠ABC=ADC∠。请用所学的知识给予说明。解答7.如图(5)∠CAE=BAD∠,∠B=D∠,AC=AE,△ABC与△ADE全等吗?为什么?ACEBD解答解答186.如图(4)AE=CF,∠AFD=∠CEB,DF=BE,△AFD与△CEB全等吗?为什么?解: AE=CF(已知)ADBCFE∴AE-FE=CF-EF(等量减等量,差相等)即AF=CE在△AFD和△CEB中,∴△AFDCEB≌△∠AFD=CEB(∠已知)DF=BE(已知)AF=CE(已证)(SAS)197.如图(5)∠CAE=BAD∠,∠B=D∠,AC=AE,△ABC与△ADE全等吗?为什么?ACEBD解: ∠CAE=BAD∠(已知)∴∠CAE+BAE∠=BAD+∠BAE∠(等量减等量,差相等)即∠BAC=DAE∠在△ABC和△ADE中,∴△ABC≌ADE△∠BAC=DAE(∠已证)AC=AE(已知)∠B=D(∠已知)(AAS)208.“三月三,放风筝”如图(6)是小东同学自己做的风筝,他根据AB=AD,BC=DC,不...