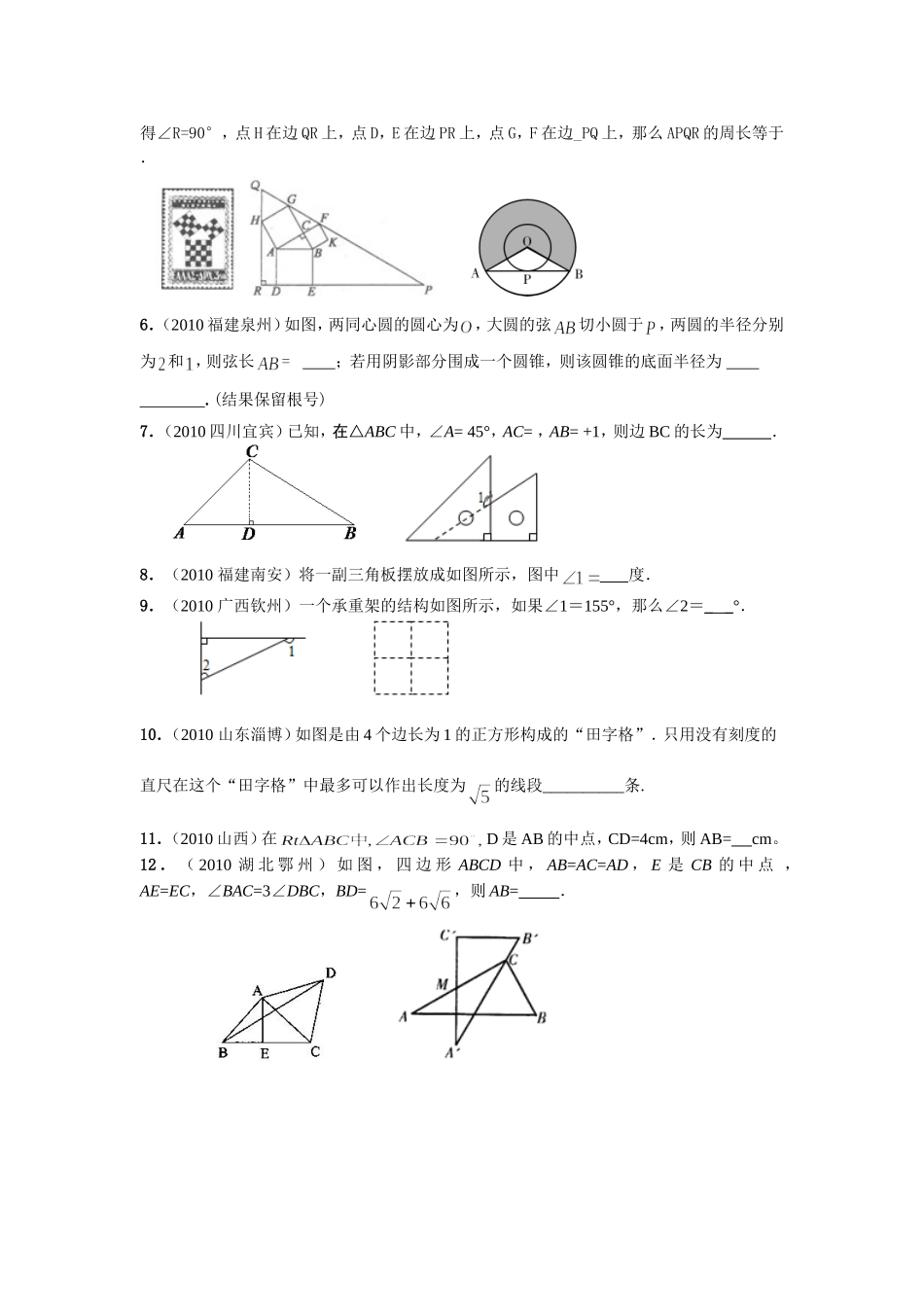
几何计算问题【备考点睛】几何计算问题常见的有:求线段的长、求角的度数,、求图形的面积等。研究几何图形及其和相关的问题时,“几何计算”具有广泛的意义:一、几何图形的大小及形状、几何图形间的位置关系,在许多时候本来就需要运用相关的数量来表示,无疑地就会涉及到几何量的计算;二、当我们注重研究图形的动点问题,图形的变换及运动问题,在坐标系里研究图形的一些问题时,就愈是不可避免地要借助几何量的计算;三、那些基于实际而模型化为几何图形的应用类问题,更是必须依靠几何量的计算来解决。几何计算是深入研究图形性质和图形间关系的重要手段,是用代数形式刻划变动中图形性质的主要凭借。也就是说,许多以图形为基础的研究性问题,许多几何与代数相结合的问题,许多图形的变换及其它形式运动的问题,都是以计算为基础,为依据,为桥梁。因此几何计算问题就成了中考中不得不考的一类问题,在填空选择各类题型中都可以体现,且往往会多处出现。1.(2010湖南益阳)如图,在△ABC中,AB=AC=8,AD是底边上的高,E为AC中点,则DE=.2.(2010浙江台州)如图,菱形ABCD中,AB=2,∠C=60°,菱形ABCD在直线l上向右作无滑动的翻滚,每绕着一个顶点旋转60°叫一次操作,则经过36次这样的操作菱形中心O所经过的路径总长为(结果保留π).3.(2010辽宁丹东)已知△ABC是边长为1的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,第n个等腰直角三角形的斜边长是.4.(2010河南)如图.矩形ABCD中,AB=1,AD=.以AD的长为半径的⊙A交BC边于点E,则图中阴影部分的面积为.5.(2010浙江温州)勾股定理有着悠久的历史,它曾引起很多人的兴趣.l955年希腊发行了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在右图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQR使得∠R=90°,点H在边QR上,点D,E在边PR上,点G,F在边_PQ上,那么APQR的周长等于.6.(2010福建泉州)如图,两同心圆的圆心为,大圆的弦切小圆于,两圆的半径分别为和,则弦长=;若用阴影部分围成一个圆锥,则该圆锥的底面半径为.(结果保留根号)7.(2010四川宜宾)已知,在△ABC中,∠A=45°,AC=,AB=+1,则边BC的长为.8.(2010福建南安)将一副三角板摆放成如图所示,图中度.9.(2010广西钦州)一个承重架的结构如图所示,如果∠1=155°,那么∠2=__°.10.(2010山东淄博)如图是由4个边长为1的正方形构成的“田字格”.只用没有刻度的直尺在这个“田字格”中最多可以作出长度为的线段__________条.11.(2010山西)在D是AB的中点,CD=4cm,则AB=cm。12.(2010湖北鄂州)如图,四边形ABCD中,AB=AC=AD,E是CB的中点,AE=EC,∠BAC=3∠DBC,BD=,则AB=.