求数列通项方法VIP免费

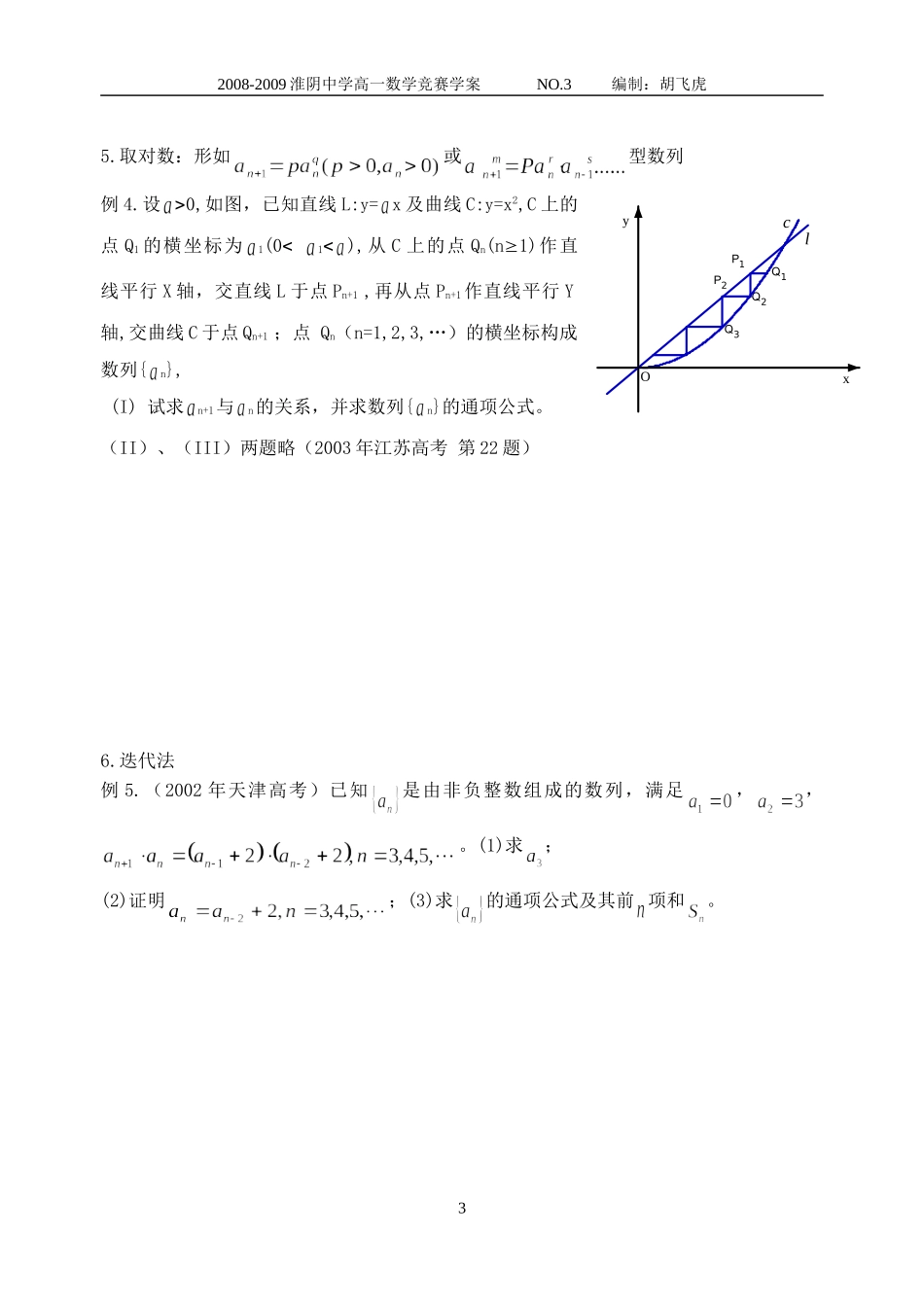
2008-2009淮阴中学高一数学竞赛学案NO.3编制：胡飞虎求数列的通项公式[本节重点]：求通项方法：叠加（乘）法、迭代法、特征根法、构造新数列[典例练讲]1.叠加法、叠乘法⑴形如，通项求法为.⑵形如，通项求法为.2.退位相减法：形如的数列3.特征根法⑴形如是常数）的数列例1.已知数列满足，求数列的通项变式：已知数列满足，求数列的通项12008-2009淮阴中学高一数学竞赛学案NO.3编制：胡飞虎⑵形如的数列例2.已知数列满足，求数列的通项变式：已知数列满足，求数列的通项4.待定系数法：①；②型数列例3.数列满足，且=1，求通项公式.变式：已知，求通项公式22008-2009淮阴中学高一数学竞赛学案NO.3编制：胡飞虎5.取对数：形如或型数列例4.设0,如图，已知直线L:y=x及曲线C:y=x2,C上的点Q1的横坐标为1(01),从C上的点Qn(n1)作直线平行X轴，交直线L于点Pn+1,再从点Pn+1作直线平行Y轴,交曲线C于点Qn+1；点Qn（n=1,2,3,…）的横坐标构成数列{n},(I)试求n+1与n的关系，并求数列{n}的通项公式。（II）、（III）两题略（2003年江苏高考第22题）6.迭代法例5.（2002年天津高考）已知是由非负整数组成的数列，满足，，。(1)求；(2)证明；(3)求的通项公式及其前项和。3Q2Q3Q1P1P2xOylc2008-2009淮阴中学高一数学竞赛学案NO.3编制：胡飞虎7.取倒数例6.数列中，，求通项公式[随堂练习]1.已知数列{an}中，an>0,且对于任意正整数n有，求通项公式an2.在数列中，，,求的通项公式an3.数列满足求4.设为实数，是方程的两个实根，数列满足，，（…）．（1）证明：，；（2）求数列42008-2009淮阴中学高一数学竞赛学案NO.3编制：胡飞虎的通项公式；（3）若，，求的前项和5.设n0，1=5，当n2时，n+n-1=+6,求数列的通项公式n。5