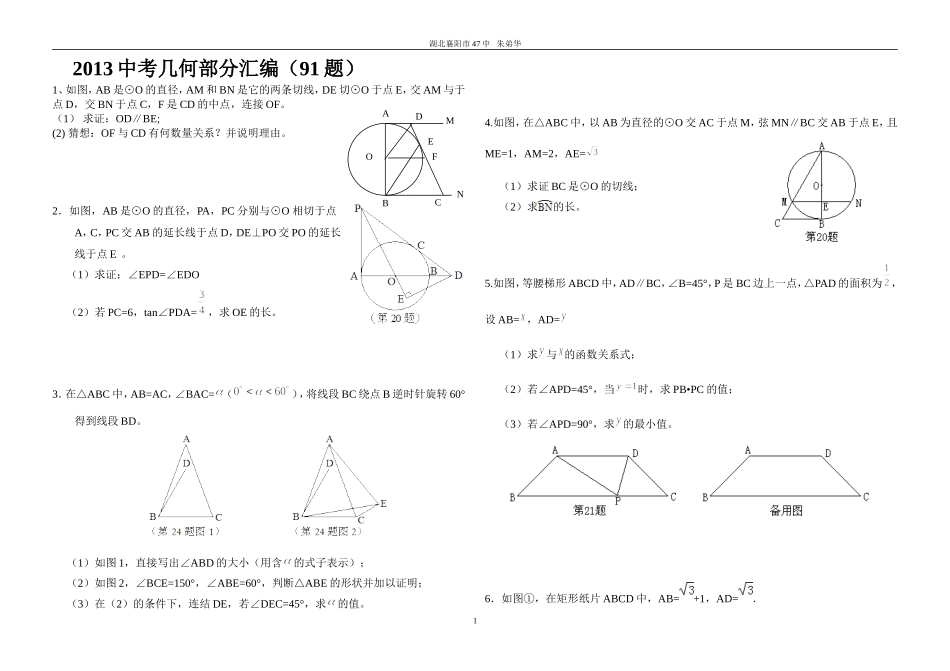
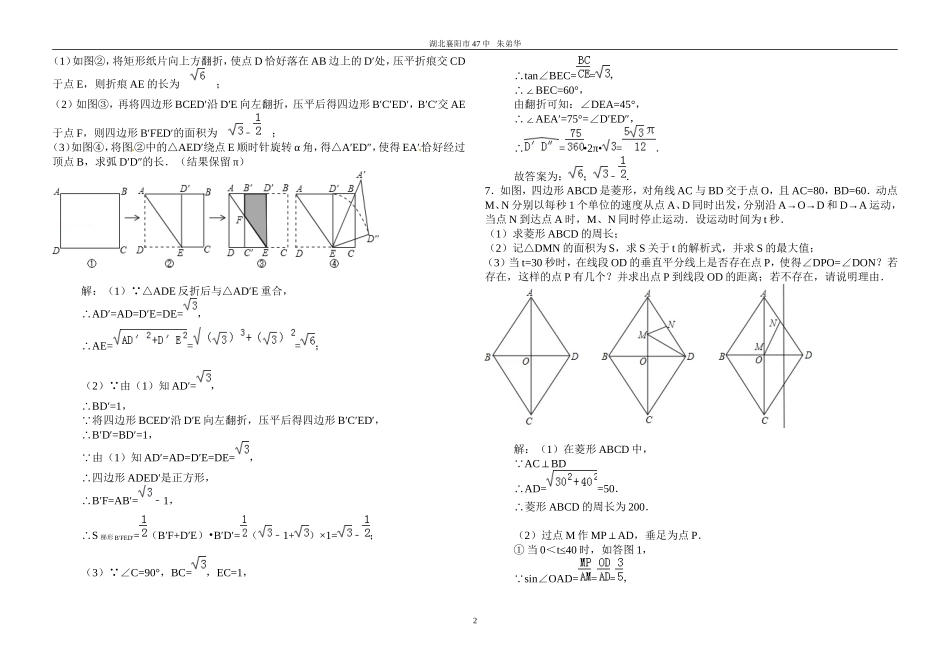
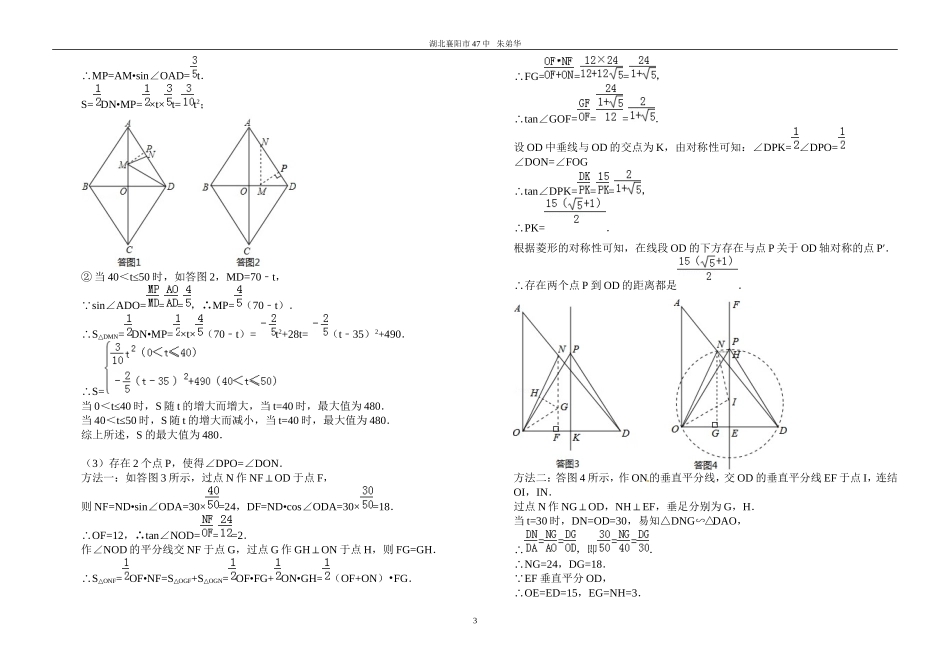
ANCBDEFMOO湖北襄阳市47中朱弟华2013中考几何部分汇编(91题)1、如图,AB是⊙O的直径,AM和BN是它的两条切线,DE切⊙O于点E,交AM与于点D,交BN于点C,F是CD的中点,连接OF。(1)求证:OD∥BE;(2)猜想:OF与CD有何数量关系?并说明理由。2.如图,AB是⊙O的直径,PA,PC分别与⊙O相切于点A,C,PC交AB的延长线于点D,DE⊥PO交PO的延长线于点E。(1)求证:∠EPD=∠EDO(2)若PC=6,tan∠PDA=,求OE的长。3.在△ABC中,AB=AC,∠BAC=(),将线段BC绕点B逆时针旋转60°得到线段BD。(1)如图1,直接写出∠ABD的大小(用含的式子表示);(2)如图2,∠BCE=150°,∠ABE=60°,判断△ABE的形状并加以证明;(3)在(2)的条件下,连结DE,若∠DEC=45°,求的值。4.如图,在△ABC中,以AB为直径的⊙O交AC于点M,弦MN∥BC交AB于点E,且ME=1,AM=2,AE=(1)求证BC是⊙O的切线;(2)求的长。5.如图,等腰梯形ABCD中,AD∥BC,∠B=45°,P是BC边上一点,△PAD的面积为,设AB=,AD=(1)求与的函数关系式;(2)若∠APD=45°,当时,求PB•PC的值;(3)若∠APD=90°,求的最小值。6.如图①,在矩形纸片ABCD中,AB=+1,AD=.1湖北襄阳市47中朱弟华(1)如图②,将矩形纸片向上方翻折,使点D恰好落在AB边上的D′处,压平折痕交CD于点E,则折痕AE的长为;(2)如图③,再将四边形BCED′沿D′E向左翻折,压平后得四边形B′C′ED′,B′C′交AE于点F,则四边形B′FED′的面积为﹣;(3)如图④,将图②中的△AED′绕点E顺时针旋转α角,得△A′ED″,使得EA′恰好经过顶点B,求弧D′D″的长.(结果保留π)解:(1) △ADE反折后与△AD′E重合,∴AD′=AD=D′E=DE=,∴AE===;(2) 由(1)知AD′=,∴BD′=1, 将四边形BCED′沿D′E向左翻折,压平后得四边形B′C′ED′,∴B′D′=BD′=1, 由(1)知AD′=AD=D′E=DE=,∴四边形ADED′是正方形,∴B′F=AB′=1﹣,∴S梯形B′FED′=(B′F+D′E)•B′D′=(﹣1+)×1=﹣;(3) ∠C=90°,BC=,EC=1,∴tan∠BEC==,∴∠BEC=60°,由翻折可知:∠DEA=45°,∴∠AEA′=75°=∠D′ED″,∴=•2π•=.故答案为:;﹣.7.如图,四边形ABCD是菱形,对角线AC与BD交于点O,且AC=80,BD=60.动点M、N分别以每秒1个单位的速度从点A、D同时出发,分别沿A→O→D和D→A运动,当点N到达点A时,M、N同时停止运动.设运动时间为t秒.(1)求菱形ABCD的周长;(2)记△DMN的面积为S,求S关于t的解析式,并求S的最大值;(3)当t=30秒时,在线段OD的垂直平分线上是否存在点P,使得∠DPO=∠DON?若存在,这样的点P有几个?并求出点P到线段OD的距离;若不存在,请说明理由.解:(1)在菱形ABCD中, AC⊥BD∴AD==50.∴菱形ABCD的周长为200.(2)过点M作MP⊥AD,垂足为点P.①当0<t≤40时,如答图1, sin∠OAD===,2湖北襄阳市47中朱弟华∴MP=AM•sin∠OAD=t.S=DN•MP=×t×t=t2;②当40<t≤50时,如答图2,MD=70t﹣, sin∠ADO===,∴MP=(70t﹣).∴S△DMN=DN•MP=×t×(70t﹣)=t2+28t=(t35﹣)2+490.∴S=当0<t≤40时,S随t的增大而增大,当t=40时,最大值为480.当40<t≤50时,S随t的增大而减小,当t=40时,最大值为480.综上所述,S的最大值为480.(3)存在2个点P,使得∠DPO=∠DON.方法一:如答图3所示,过点N作NF⊥OD于点F,则NF=ND•sin∠ODA=30×=24,DF=ND•cos∠ODA=30×=18.∴OF=12,∴tan∠NOD===2.作∠NOD的平分线交NF于点G,过点G作GH⊥ON于点H,则FG=GH.∴S△ONF=OF•NF=S△OGF+S△OGN=OF•FG+ON•GH=(OF+ON)•FG.∴FG===,∴tan∠GOF===.设OD中垂线与OD的交点为K,由对称性可知:∠DPK=∠DPO=∠DON=∠FOG∴tan∠DPK===,∴PK=.根据菱形的对称性可知,在线段OD的下方存在与点P关于OD轴对称的点P′.∴存在两个点P到OD的距离都是.方法二:答图4所示,作ON的垂直平分线,交OD的垂直平分线EF于点I,连结OI,IN.过点N作NG⊥OD,NH⊥EF,垂足分别为G,H.当t=30时,DN=OD=30,易知△DNG∽△DAO,∴,即.∴NG=24,DG=18. EF垂直平分OD,∴OE=ED=15,EG=NH=3.3湖北襄阳市47中朱弟华设OI=R,EI=x,则在Rt△OEI...