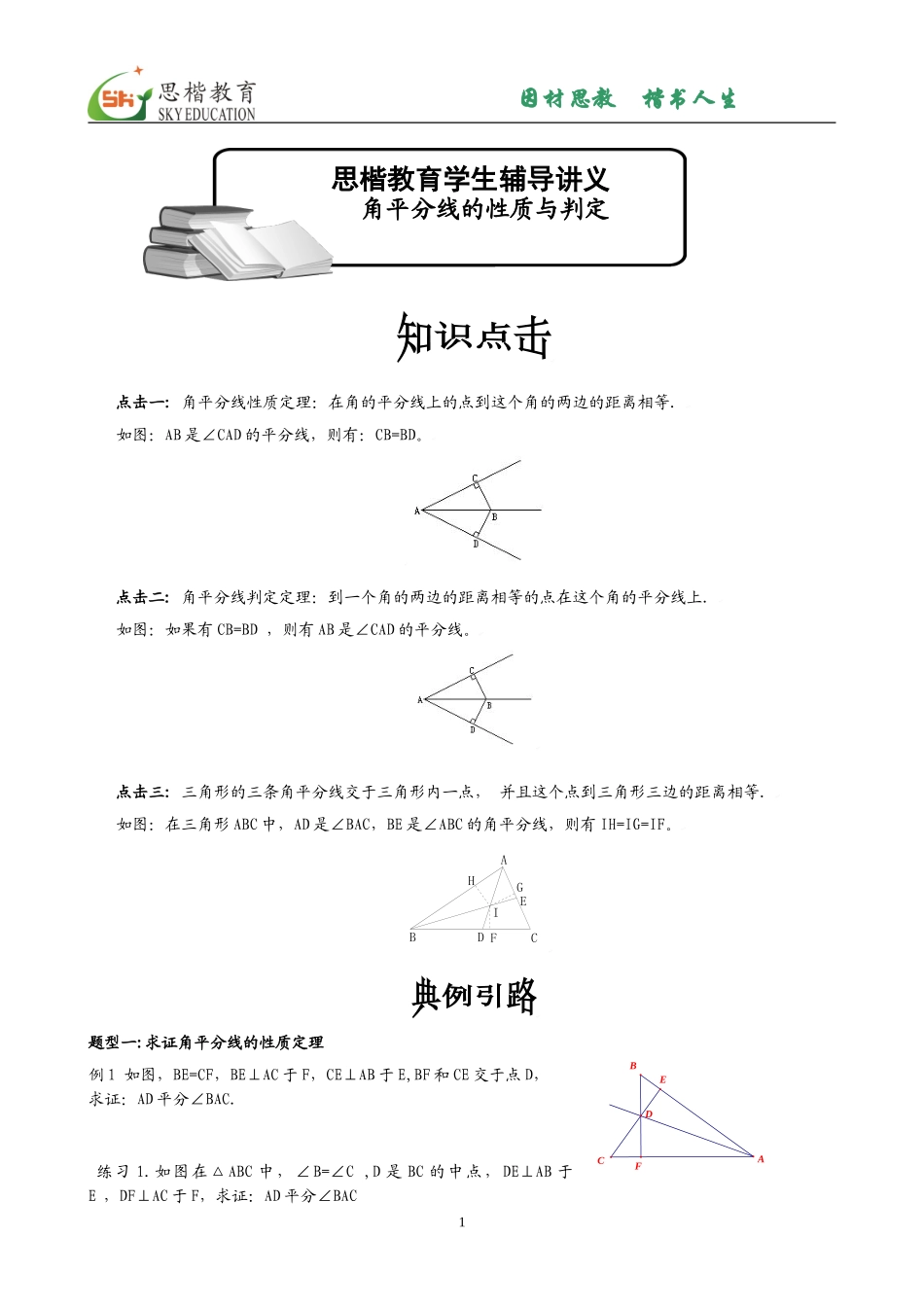
因材思教楷书人生点击一:角平分线性质定理:在角的平分线上的点到这个角的两边的距离相等.如图:AB是∠CAD的平分线,则有:CB=BD。点击二:角平分线判定定理:到一个角的两边的距离相等的点在这个角的平分线上.如图:如果有CB=BD,则有AB是∠CAD的平分线。点击三:三角形的三条角平分线交于三角形内一点,并且这个点到三角形三边的距离相等.如图:在三角形ABC中,AD是∠BAC,BE是∠ABC的角平分线,则有IH=IG=IF。DCBAEHIFG题型一:求证角平分线的性质定理例1如图,BE=CF,BE⊥AC于F,CE⊥AB于E,BF和CE交于点D,求证:AD平分∠BAC.练习1.如图在△ABC中,∠B=∠C,D是BC的中点,DE⊥AB于E,DF⊥AC于F,求证:AD平分∠BAC1CEDFAB思楷教育学生辅导讲义角平分线的性质与判定因材思教楷书人生练习2.如图BE⊥AC于E,CF⊥AB于F,BE,CF相交于点D,且CE=BF,求证:点D在∠BAC的平分线上例2.如图,在△ABC中,∠C=90。,AD平分∠BAC,DE⊥AB于E,F在AC上,BD=DF,求证:CF=EB练习如图,在Rt△ABC中,∠C=90。,AC=BC,AD为∠BAC的平分线,AE=BC,DE⊥AB,垂足为E,求证△DBE的周长等于AB.题型二、辅助线习题例3如图,在△ABC中,外角∠CBE和∠BCG的平分线相交于点F,求证:点F在∠BAC的平分线上例4如图,已知∠B=∠C=90。,DM平分∠ADC,AM平分∠DAB,探究线段BM与CM的关系,说明理由。例5已知:如图在△ABC中,BD=DC,∠1=∠2,求证:AD平分∠BAC.例6如图,AB=AC,BD=CD,DE⊥AB于E,DF⊥AC于F,求证:DE=DF类型三:利用角平分线的性质求线段之比例7:如图,已知:∠BAC=30,G为∠BAC的平分线上的一点,若EG∥AC交AB于E,GD⊥AC于D,GD:GE=()2FEDABCCDEBFAFEAGBCBCMADEDACBF21BCADBEFDCBDCAE因材思教楷书人生类型四:利用角平分线的性质求角的度数例8:在△ABC中,∠ABC=100,∠ACB=20,CE平分∠ACB交AB于E,D在AC上,且∠CBD=20。求∠CED的度数。【解析】此题是考查利用角平分线的性质求角的度数。【答案】作EF⊥AC,延长CB,作EG⊥CB3