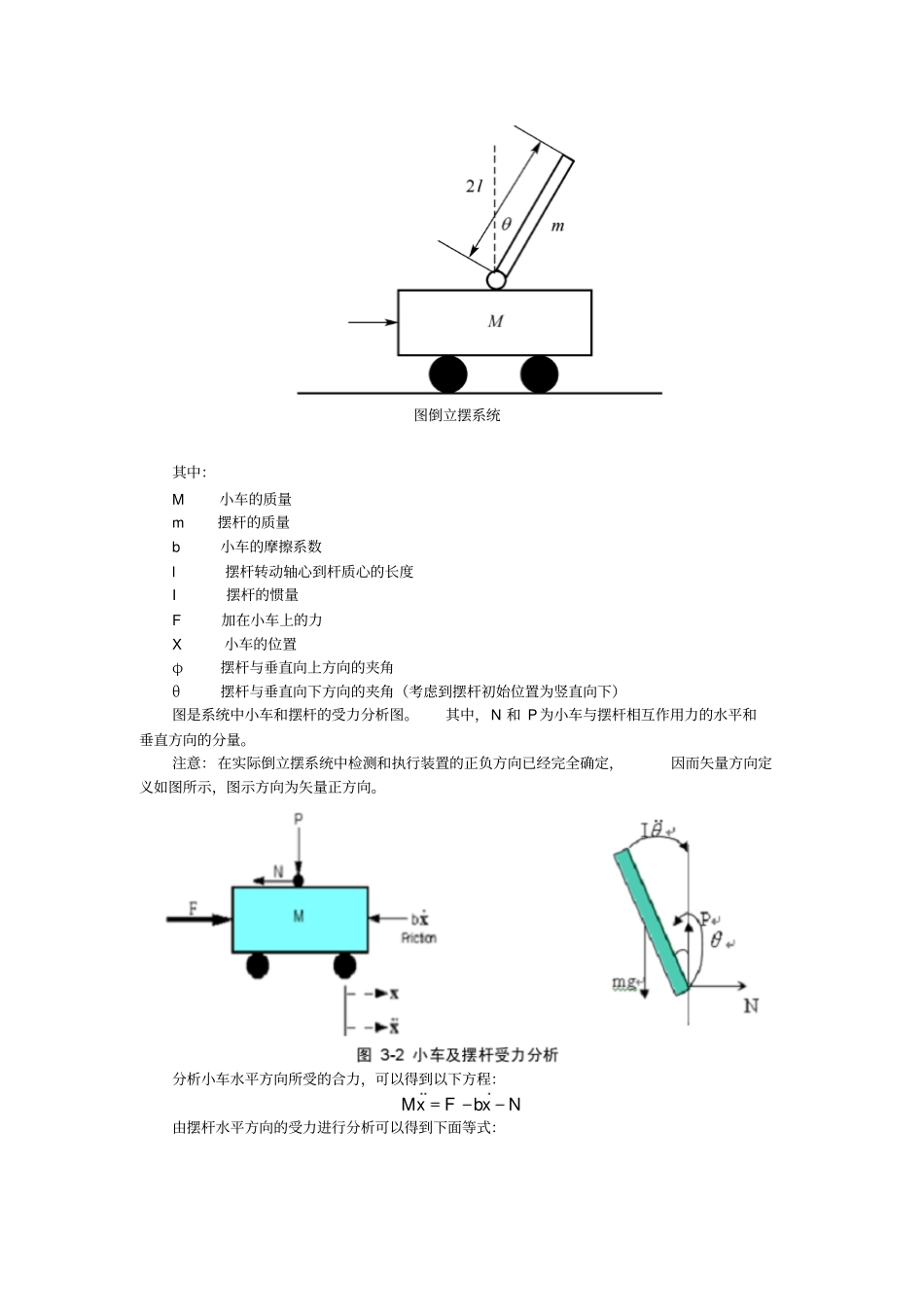
综合性实验设计题目:直线一级倒立摆班级:0802姓名:郭长春指导老师:张白莉学号:200807211065摘要倒立摆是一个复杂的多变量强祸合不稳定非线性的系统,借助于这样一个系统可以有效的检测各种控制理论的好坏。本论文研究了倒立摆系统的建模方法,采用Lagrange方程对一级倒立摆系统进行建模。针对倒立摆的状态空间方程,采用MatLab软件对倒立摆的稳定性,能控性,能观性和可控度做了分析;采用最优控制理论对倒立摆系统进行稳摆控制并进行仿真,并利用该理论将倒立摆的数学模型加以改进,并对改进后的倒立。经过仿真分析确认改进后的倒立摆系统控制效果得到了明显的改善。正文1.倒立摆系统研究的背景随着各种控制理论的发展,理论的正确性,它在实际应用中的可行性,都需要用一个典型的对象来验证,这种控制对象必须能够比较各种控制理论的优劣。倒立摆系统就是我们需要的理想的实验控制平台。倒立摆控制系统,是一个复杂的多变量强祸合不稳定非线性系统。对倒立摆系统进行研究,能有效的反映控制策略中的许多典型问题,,针对倒立摆而研究的控制方法在双足机器人的行走平衡方面、军工方面、火箭发射过程的垂直度控制、卫星在飞行中的姿态控制以及日常生产过程和生活领域中的应用都非常广泛。因此,倒立摆系统的研究,有着重要的工业背景和实际意义。2.直线一级倒立摆系统的建模直线一级倒立摆的工作原理可简述为:用一种强有力的控制方法使小车以一定的规律来回运动,从而使摆杆在垂平面内稳定下来。这样的系统就是倒立摆的控制系统如下图所示若小车不动,摆杆会由于重力作用倒下来若在水平方向给小车一个力,则摆杆受到一个力矩,这个力矩使摆杆朝与小车相反的方向运动,通过规律性的改变小车的受力方向使得摆杆在竖直方向左右摆动从而实现摆杆在竖直方向的动态平衡。在忽略了空气阻力和各种摩擦之后,可将直线一级倒立摆系统抽象成小车和匀质杆组成的系统。如下如所示。图倒立摆系统其中:M小车的质量m摆杆的质量b小车的摩擦系数l摆杆转动轴心到杆质心的长度I摆杆的惯量F加在小车上的力X小车的位置φ摆杆与垂直向上方向的夹角θ摆杆与垂直向下方向的夹角(考虑到摆杆初始位置为竖直向下)图是系统中小车和摆杆的受力分析图。其中,N和P为小车与摆杆相互作用力的水平和垂直方向的分量。注意:在实际倒立摆系统中检测和执行装置的正负方向已经完全确定,因而矢量方向定义如图所示,图示方向为矢量正方向。分析小车水平方向所受的合力,可以得到以下方程:NxbFxM由摆杆水平方向的受力进行分析可以得到下面等式:)sin(22lxdtdmN即:sincos2mlmlxmN把这个等式代入式(3-1)中,就得到系统的第一个运动方程:FmlmlxbxmMsincos)(2为了推出系统的第二个运动方程,我们对摆杆垂直方向上的合力进行分析,可以得到下面方程:)cos(22ldtdmmgPcossin2mlmlmgP力矩平衡方程如下:INlPlcossin注意:此方程中力矩的方向,由于sinsin,coscos,,故等式前面有负号。合并这两个方程,约去P和N,得到第二个运动方程:cossin)(2xmlmglmlI设(是摆杆与垂直向上方向之间的夹角),假设与1(单位是弧度)相比很小,即1,则可以进行近似处理:0)(,sin,1cos2dtd。用u来代表被控对象的输入力F,线性化后两个运动方程如下:2(+)()ImlmglmlxMmxbxmlu对式(3-9)进行拉普拉斯变换,得到2111011(+)()JmLmglmLrmmrrmLu3.传递函数模型推导传递函数时假设初始条件为0。由于输出为角度,求解方程组的第一个方程,可以得到:21121()()[]()JmLgRssmLs或2122111()()()smLsRsJmLsmgL(18-10)如果令xv,则有:122111()()()smLVsJmLsmgL把上式代入方程组的第二个方程,得到:222111101211()()()()()()JmLgJmLgmmssmlssUsmLsmLs整理后得到传递函数:212432110111()()()()mLssqJmLmmmgLmgLUsssssqqq(18-11)其中2201111()()()qmmJmLmL4.状态空间方程模型设系统状态空间方程为:DuCXyBuAXX方程组对,x解代数方程,得到解如下:2222111112221001101011010111011222101011010110110()()()()()()()()()xxJmLmgLJmLxxuJmmmmLJmmmmLJmmmmLmLmgLmmmLxuJmmmmLJmmmmLJmmmmL整理后得到系统状态空间方程:2222111112221010110101101011...