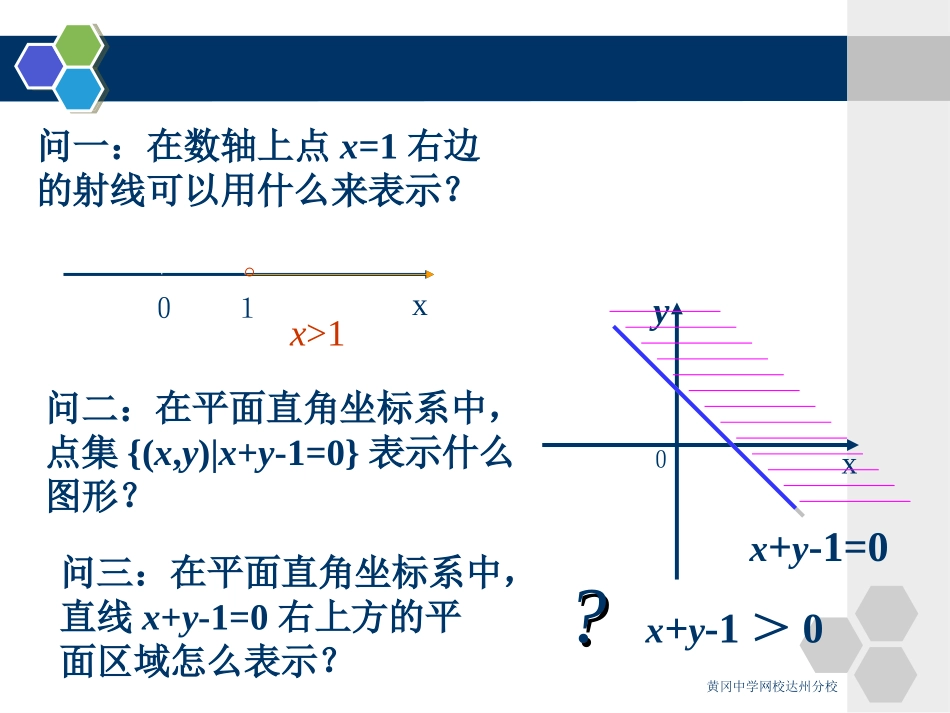
黄冈中学网校达州分校§7.4.1简单的线性规划(一)黄冈中学网校达州分校教学目标1.理解二元一次不等式表示的平面区域.2.会根据二元一次不等式确定它所表示的平面区域,并能画出二元一次不等式(组)表示的平面区域.3.能把若干直线围成的平面区域用二元一次不等式组表示.教学重点:理解如何用二元一次不等式(组)表示平面区域.教学难点:如何确定二元一次不等式表示的平面区域.黄冈中学网校达州分校问一:在数轴上点x=1右边的射线可以用什么来表示?x>1问二:在平面直角坐标系中,点集{(x,y)|x+y-1=0}表示什么图形?问三:在平面直角坐标系中,直线x+y-1=0右上方的平面区域怎么表示???x+y-1>0x+y-1=00xy10x黄冈中学网校达州分校直线x+y-1=0右上方的平面区域怎么表示???x+y-1>0x+y-1=00xyxyx+y-1>011是12是20是21是22是……猜想:猜想:x+y-1>0黄冈中学网校达州分校思路一:在直线右上方任取一点(x,y),过此点作一平行x轴的直线x+y-1=00xyP0(x0,y0)(x,y)思路二:在直线右上方任取一点(x,y),过此点作一平行y轴的直线x+y-1=00xyP0(x0,y0)(x,y)x>x0,y=y0x+y>x0+y0x+y-1>x0+y0-1=0x=x0,y>y0x+y>x0+y0x+y-1>x0+y0-1=0黄冈中学网校达州分校直线x+y-1=0右上方的平面区域可以用点集{(x,y)|x+y-1>0}表示直线x+y-1=0左下方的平面区域可以用点集{(x,y)|x+y-1<0}表示x+y-1=00xyx+y-1>0x+y-1<0黄冈中学网校达州分校二元一次不等式表示的平面区域Oxy在平面直角坐标系中,以二元一次方程x+y-1=0的解为坐标的点的集合{(x,y)|x+y-1=0}是经过点(0,1)和(1,0)的一条直线l,那么以二元一次不等式x+y-1>0的解为坐标的点的集合{(x,y)|x+y-1>0}是什么图形?11x+y-1=0探索结论x+y-1>0x+y-1<0黄冈中学网校达州分校结论:二元一次不等式ax+by+c>0在平面直角坐标系中表示直线ax+by+c=0某一侧所有点组成的平面区域.不等式ax+by+c<0表示的是另一侧的平面区域.黄冈中学网校达州分校结论:一般地,二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域。我们把直线画成虚线以表示区域不包含边界直线。(同侧同号)小结:概括地说,判断方法为“直线定界,特殊点定域”。特别地C≠0时,常把原点作为特殊点,即“直线定界,原点定域”。黄冈中学网校达州分校判断二元一次不等式表示哪一侧平面区域的方法:方法一:取特殊点检验;如果不等式所对应直线不经过(0,0),则一般取原点作为特殊点代入.方法二:若不等式可化为ykx+b的形式,则此不等式表示直线上方的平面区域;黄冈中学网校达州分校判断二元一次不等式表示哪一侧平面区域的方法Oxy11x+y-1=0x+y-1>0x+y-1<0由于对在直线ax+by+c=0同一侧所有点(x,y),把它的坐标(x,y)代入ax+by+c,所得的实数的符号都相同,故只需在这条直线的某一侧取一特殊点(x0,y0)以ax0+by0+c的正负的情况便可判断ax+by+c>0表示这一直线哪一侧的平面区域,特殊地,当c≠0时常把原点作为此特殊点.黄冈中学网校达州分校例1画出不等式2x+y-6<0表示的平面区域.Oxy36注意:把直线画成虚线以表示区域不包括边界2x+y-6=0黄冈中学网校达州分校例2.画出不等式组表示的平面区域.3005xyxyxOxy35x-y+5=0x+y=0x=3黄冈中学网校达州分校例3.画出不等式组表示的平面区域。53006xyyxyxx=5x-y=0y=3CBA665x+y-6=003xy黄冈中学网校达州分校二元一次不等式表示平面区域小结由于对在直线ax+by+c=0同一侧所有点(x,y),把它的坐标(x,y)代入ax+by+c,所得的实数的符号都相同,故只需在这条直线的某一侧取一特殊点(x0,y0)以ax0+by0+c的正负的情况便可判断ax+by+c>0表示这一直线哪一侧的平面区域,特殊地,当c≠0时常把原点作为此特殊点.练习1:思考并回答下列各集合所表示的点的集合分别是什么图形?⑴{(x,y)|x=0};{(x,y)|x>0};{(x,y)|x≤0}⑵{(x,y)│y=0};{(x,y)│y>0};{(x,y)│y≤0}(Y轴)OXYXYXYOOOXYOXYOXY(Y轴右方的平面区域,不含边界线)(Y轴左方的平面区域,含边界线)(X轴)(X轴上方的平面区域,不含边界线)...