第4课时圆周角(1)VIP免费

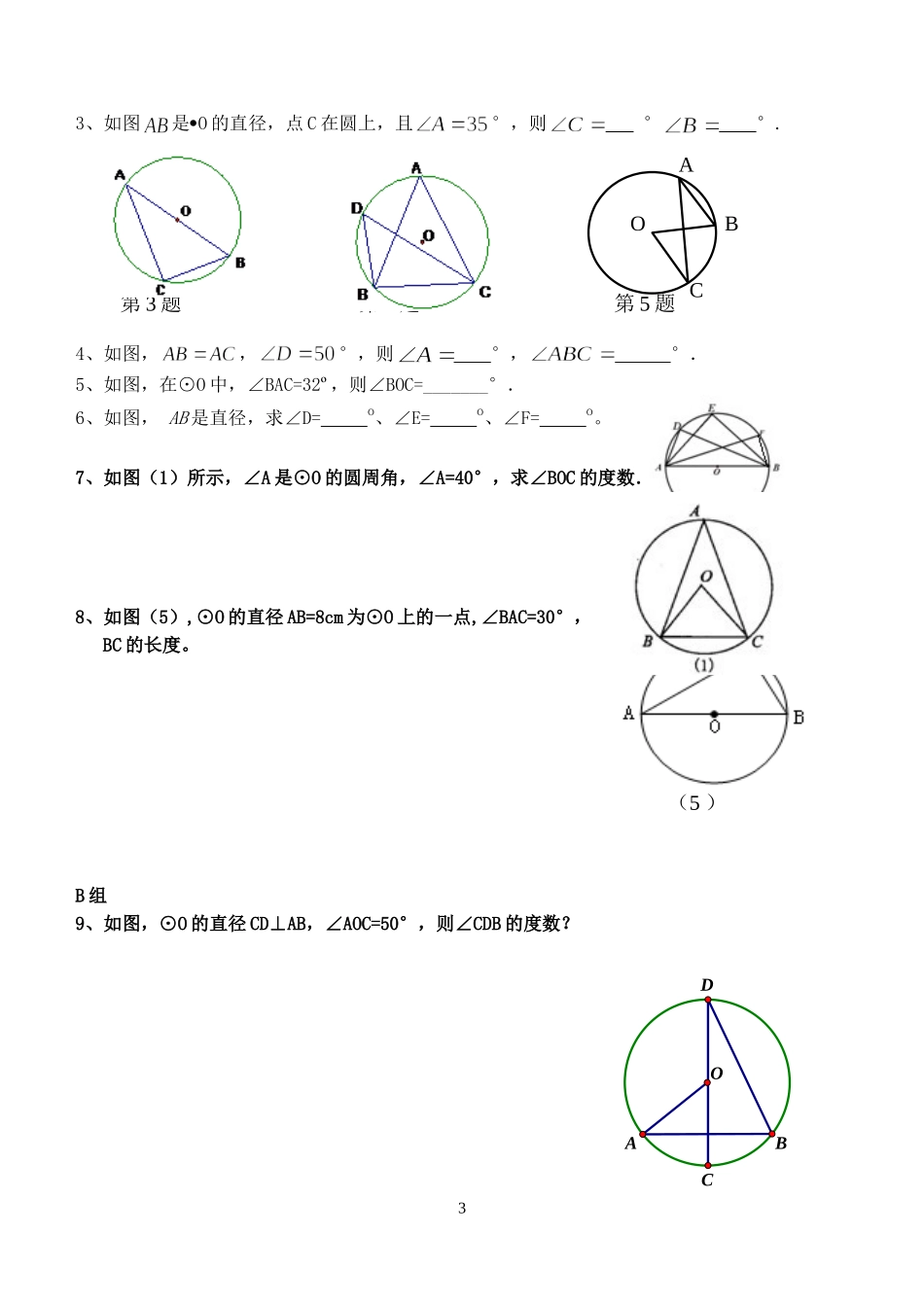
OABC第4课时圆周角（1）班级姓名学号（一）学习目标：能判断一个角是否是圆周角，参与圆周角定理的证明，感受转化和分类的数学思想，会根据圆周角定理找等角。（二）课前小测：1、如图，在⊙O中，弧AB=弧BC，AB=4,∠AOB=70°，则BC=，∠AOC=2、复习导入：什么是圆心角？（三）探索新知1、如图，∠AOB是角，它所对的弧是，∠ACB与∠AOB有何异同点？类似地，你能给像∠ACB这一类的角起一个合适的名字吗？（提示：圆心角是因为角的顶点位置而命名的。）2、圆周角定义：课本P84两个基本特征：(1)顶点在上，（2）两边都与圆。3、判断下列各图的角是否圆周角？4、探究：现在通过圆周角的概念和度量的方法回答下面的问题．（1）一条弧所对的圆周角的个数有多少个？（2）同弧所对的圆周角的度数是否发生变化？（3）同弧上的圆周角与圆心角有什么关系？※5、在圆上任取一个圆周角，观察圆心与圆周角的位置关系有几种情况？你能选择一种情况证明你猜测的数量关系。6、归纳圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半。7、圆周角定理几何表述：1DBDAC图1EDCAB图2COAB图3CAB图4OCBAO18050CAB2OCBA553O(1)∵弧CD=弧CD(2)∵弧CD=弧DE(3)∵(4)∵∴∠A=∠B∴∴∴8、直径所对的圆周角请在右边画⊙O与其直径AB，任意画一个圆周角∠ACB，猜想它的度数。并交流你的理由。结论：直径所对的圆周角等于度；所对的弦是直径。（四）例题如图（4）,点D在以AC为直径的⊙O上,如果∠BDC=20°，求∠ACB的度数.巩固练习A组1、看图求角．∠1=∠2=∠3=2、如图，（1）若∠AOB=1000，∠D=°，∠C=°；（2）若∠D=500，∠AOB=°，∠C=°；2（4）第3题第4题第5题（5）3、如图是O的直径，点C在圆上，且°，则°°.4、如图，，°，则°，°．5、如图，在⊙O中，∠BAC=32º，则∠BOC=_______°．6、如图，AB是直径，求∠D=o、∠E=o、∠F=o。7、如图（1）所示，∠A是⊙O的圆周角，∠A=40°，求∠BOC的度数．8、如图（5）,⊙O的直径AB=8cm为⊙O上的一点,∠BAC=30°，BC的长度。B组9、如图，⊙O的直径CD⊥AB，∠AOC=50°，则∠CDB的度数？3OABDCAOCB