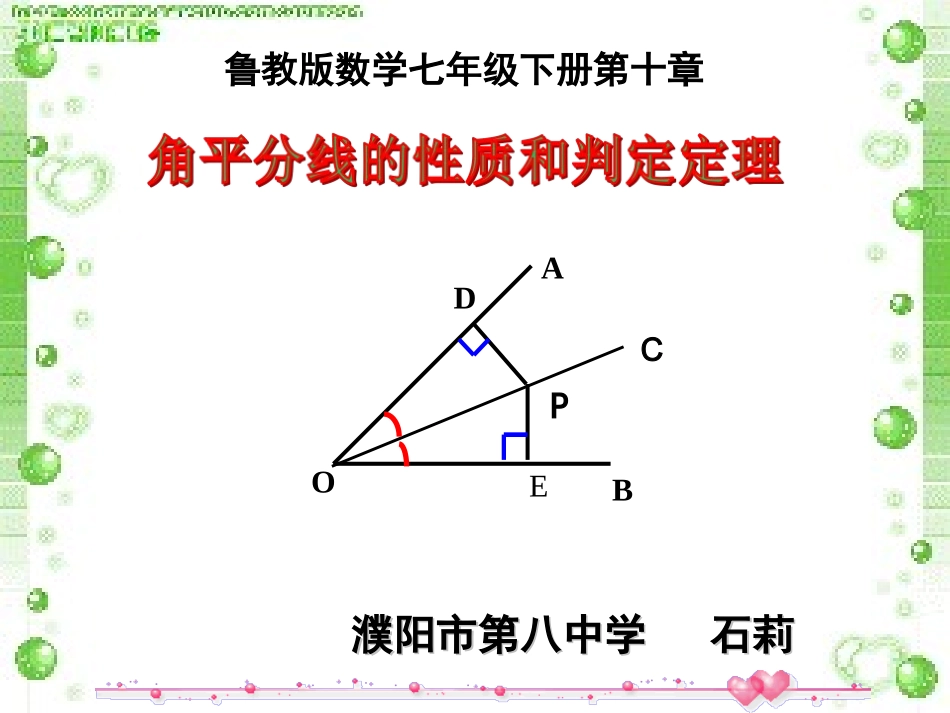
濮阳市第八中学石莉濮阳市第八中学石莉鲁教版数学七年级下册第十章DPEAOBC假如要在三角形区域建造一个观景台,使得该位置中心到三边的距离相等,你能确定该位置中心吗三角公园1、“角平分线”的定义.2、做一个角的平分线的方法.3、点到直线的距离.角的平分线:从一个角的顶点引出一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.oBCA123、尺规作图AABBOOMMNNCC做一个角的平分线的方法1、用量角器度量2、用折纸的方法从直线外一点,到这条直线的垂线段的长度叫做点到直线的距离.OPAB点到直线的距离预习交流请师友小组交流本节课的预习情况1、学师帮助学友解决预习中的问题.2、学师不会的可以向其他组的学师求助,或向老师求助.在角的平分线上任取一点P,过点P画出角的两边的垂线,分别记垂足为D、E,猜想PD、PE的大小关系.PD=PE质疑探究DPEAOBC已知:如图,OC是∠AOB的平分线,点P在OC上,PDOA⊥,PEOB⊥,垂足分别是D,E.求证:PD=PE.证明:∵PDOA⊥,PEOB⊥(已知)∴∠PDO=PEO=90∠°(垂直的定义)在△PDO和△PEO中∴PD=PE(全等三角形的对应边相等).∠PDO=PEO∠∠POD=POE∠OP=OP∴△PDO≌PEO△(AAS)角平分线上的点到这个角的两边的距离相等.DPEAOBC角平分线的性质定理——角平分线上的点到这个角的两边的距离相等角平分线上的点到这个角的两边的距离相等..∴PD=PE.几何语言∵OP平分∠AOB,PD⊥OA于点D,PE⊥OB于点E.BADOPE定理的作用:证明线段相等EAOBDPC已知:如图,PD⊥OA,PE⊥OB,点D、E为垂足,且PD=PE.求证:OP平分∠AOB.证明:∵∵PD⊥OA,PE⊥OB(已知),∴∠PDO=∠PEO=90°(垂直的定义)在Rt△PDO和Rt△PEO中PO=PO(公共边)PD=PE∴Rt△PDO≌Rt△PEO(HL)∴∠POD=∠POE∴OP平分∠AOBEAOBDPC角平分线的判定定理角平分线的判定定理∵∵PD⊥OA,PE⊥OB,PD=PE.∴OP平分∠AOB.EAOBDPC在一个角的内部,并且到角的两边距离相等的点,在这个角的平分线上.几何语言定理的作用:证明角相等例1.在△ABC中,∠BAC=60°,点D在BC上,AD=10,DE⊥AB,DF⊥AC,垂足分别为点E,F,且DE=DF,求DE的长.ABCDEF例题解:∵∵DE⊥AB,DF⊥AC,垂足分别为点E,F,且DE=DF,∴点D在∠BAC的平分线上.(在一个角的内部,并且到角的两边距离相等的点,在这个角的平分线上.)即AD平分∠BAC∵∵∠BAC=60°,∴∠BAD=30°.在Rt△ADE中,∠AED=90°,AD=10∴DE=5.ABCDEF图11.如图1,OP平分∠AOB,则PD=PE.()2.如图2,PD⊥OA于点D,PE⊥OB于点E.则PD=PE.()3.如图3,OP平分∠AOB,PD⊥OA于点D,PE⊥OB于点E,则PD=PE.()BADOPEBADOPE××垂直的条件点在角的平分线上图2√DPEAOB图3性质有两个条件,一个也不能少巩固提升1.如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到OA的距离是______.2BPCAOD二、填空题2、如图,OC平分∠AOB,PM⊥OB于点M,PN⊥OA于点N,△POM的面积为6,OM=6,则PN=_______.2MAOBNPC.P假如要在三角形区域建造一个观景台,使得该位置中心到三边的距离相等,你能确定该中心所处的位置吗归纳总结请师友小组交流本节课的收获1、自己总结本节课你学到了什么;2、师友交流,互相补充.证明线段相等.角平分线的性质定理角平分线的性质定理角平分线上的点到这个角的两边的距离相等.DPEAOBC角平分线的判定定理角平分线的判定定理在一个角的内部,并且到角的两边距离相等的点,在这个角的平分线上.证明角相等在Rt△ABC中,∠C=90°.(2)如图2,AC=BC,AB=10,将△ABC沿直线BD折叠,使点C落在AB边上的点E处,求△AED的周长.(1)如图1,BD平分∠ABC,DE⊥AB于E.若AC=6,AD+DE的值为多少?请说明理由.图1图2EDBCA10EDBCA再见