一元二次方程的根与系数的关系-(7)VIP免费

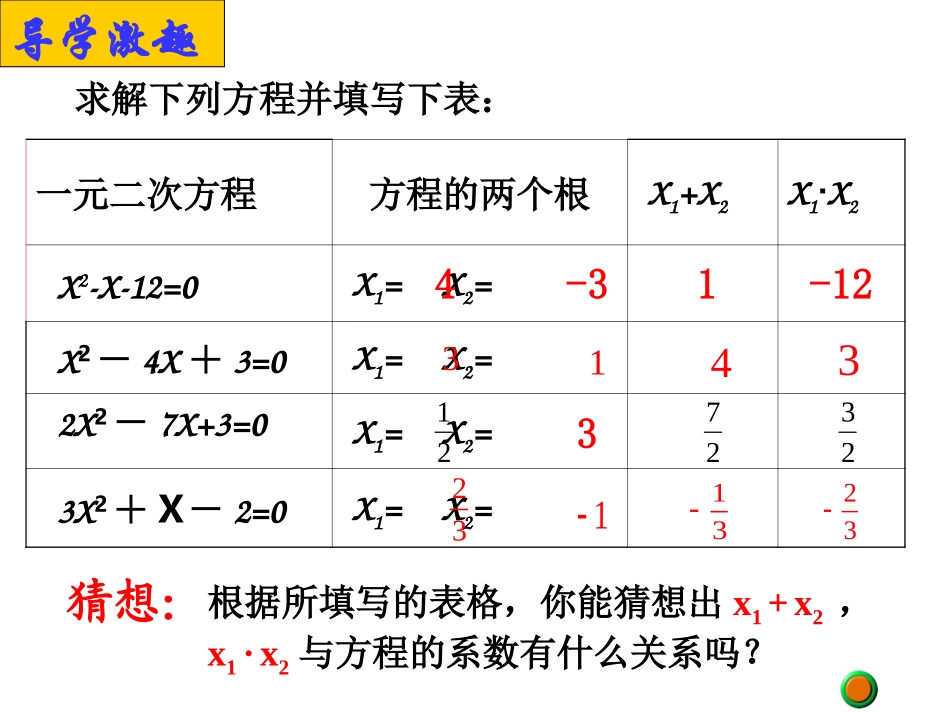
21.2.421.2.4一元二次方程一元二次方程————根与系数的关系根与系数的关系21.2.421.2.4一元二次方程一元二次方程————根与系数的关系根与系数的关系1.一元二次方程的一般形式是什么？3.一元二次方程的解的情况怎样确定？2.一元二次方程的求根公式是什么？)0(02acbxaxacb42没有实数根两个相等的实数根两个不相等的实数根000)04(2422acbaacbbx温故知新求解下列方程并填写下表：一元二次方程方程的两个根X1+X2X1·X2X2-X-12=0X1=X2=X2－4X＋3=0X1=X2=2X2－7X+3=0X1=X2=3X2＋X－2=0X1=X2=23133412313猜想：根据所填写的表格，你能猜想出x1+x2，x1·x2与方程的系数有什么关系吗？导学激趣4-331-12232721证明你的猜想已知：如果一元二次方程的两个根分别是、。1x2xacxx21abxx21求证：已知：如果一元二次方程的两个根分别是、。已知：如果一元二次方程的两个根分别是、。已知：如果一元二次方程的两个根分别是、。已知：如果一元二次方程的两个根分别是、。已知：如果一元二次方程的两个根分别是、。已知：如果一元二次方程的两个根分别是、。已知：如果一元二次方程的两个根分别是、。)0(02acbxaxabxx21已知：如果一元二次方程的两个根分别是、。)0(02acbxax求证：abxx21已知：如果一元二次方程的两个根分别是、。)0(02acbxaxacxx21求证：abxx21已知：如果一元二次方程的两个根分别是、.acaacbbaacbbaacbbxx2222222144)24()24(ababaacbbaacbbxx2224242221证明：如果一元二次方程的两个根分别是、，那么：abxx21acxx21)0(02acbxax1x2x这就是一元二次方程根与系数的关系，也叫韦达定理。归纳：注：前提条件为b2-4ac≥0韦达（1540——1603）是法国数学家,最早发现代数方程的根与系数之间有这种关系，因此，人们把这个关系称为韦达定理。韦达最重要的贡献是对代数的推进，他最早系统地引入代数符号，推进了方程论的发展。韦达用“分析”这个词来概括当时代数的内容和方法。他创设了大量的代数符号，用字母代替未知数，系统阐述并改良了三、四次方程的解法，著有《分析方法入门》、《论方程的识别与订正》等多部著作。例1、不解方程，求下列方程两根的和与积0973)2(2xx典例分析2415)3(xx0156)1(2xx运用1、直接运用根与系数的关系巩固训练:1.下列方程两根的和与两根的积各是多少(不解方程）（1）2x2+3x=0（2）3x2=1（3）x2-3x=15⒉方程的两根和为4，积为-3，则a=，b=。3.求一个一元二次方程，使它的两个根是2和3，如：。2202xaxb8-30652xx例例2:2:已知方程已知方程55x2+kx-6=0的一个根是2，求它的另一个根及k的值。解：设方程的另一个根是x1，那么2x1=-—∴x1=-—.66555533又（-—）+2=-—553355kk∴k=-5（-—）+2=-75533答：方程的另一个根是-—，k的值是-7。5533运用2、求方程另一个根及字母k的值知识源于悟例3：设是方程的两个根，利用根与系数的关系，求下列各式的值：（1）；（2）；21,xx03422xx2212xx1211xx运用3、求关于两根的对称式或代数式的值•例3（变式）设是方程的两个根，利用根与系数的关系，求下列各式的值：（1）；（2）；（3）21,xx03422xx)1)(1(21xx221221xxxx221)(xx知识源于悟例4、若关于x的一元二次方程的两个实数根分别是,且满足.求k的值.22430xkxk12,xx1212xxxx运用4根的判别式与根系关系的综合运用练习：已知关于x的方程kx2-2(k+1)x+k-1=0有两个不相等的实数根，①求k的取值范围；②是否存在实数k，使此方程的两个实数根的倒数和等于0？若存在，求出k的值；2.应用一元二次方程的根与系数的关系时，首先要把已知方程化成一般形式。3.应用一元二次方程的根与系数关系时，要特别注意，方程有实根的条件，即在初中代数里，只有当时，才能应用根与系数的关系.1.一元二次方程根与系数的关系是什么?042acb•你还有什么疑惑？质疑提问