1.3.2三角函数的图象与性质VIP免费

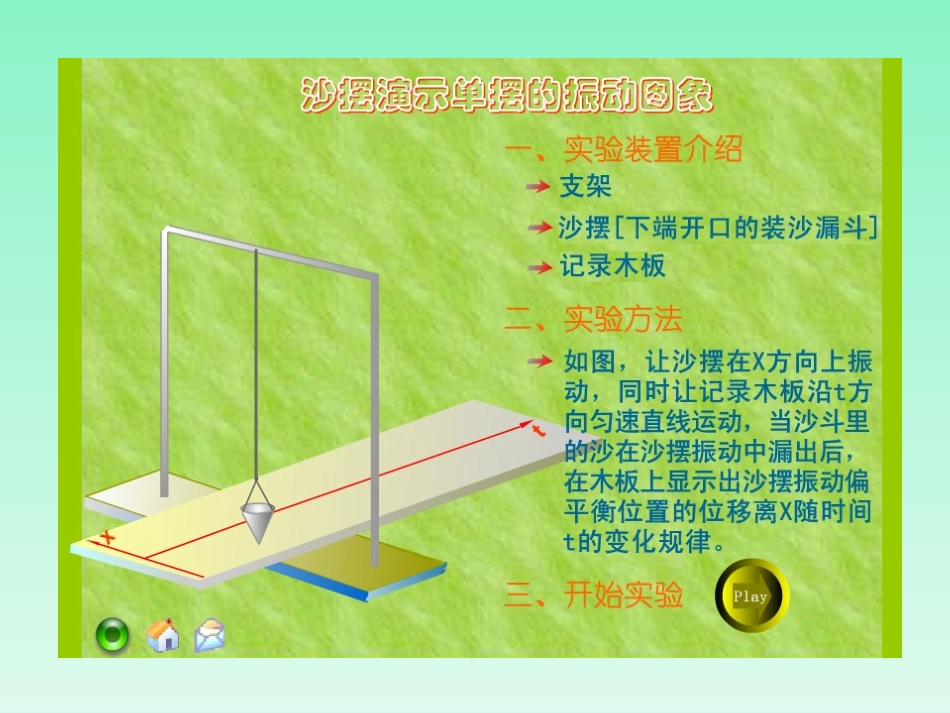
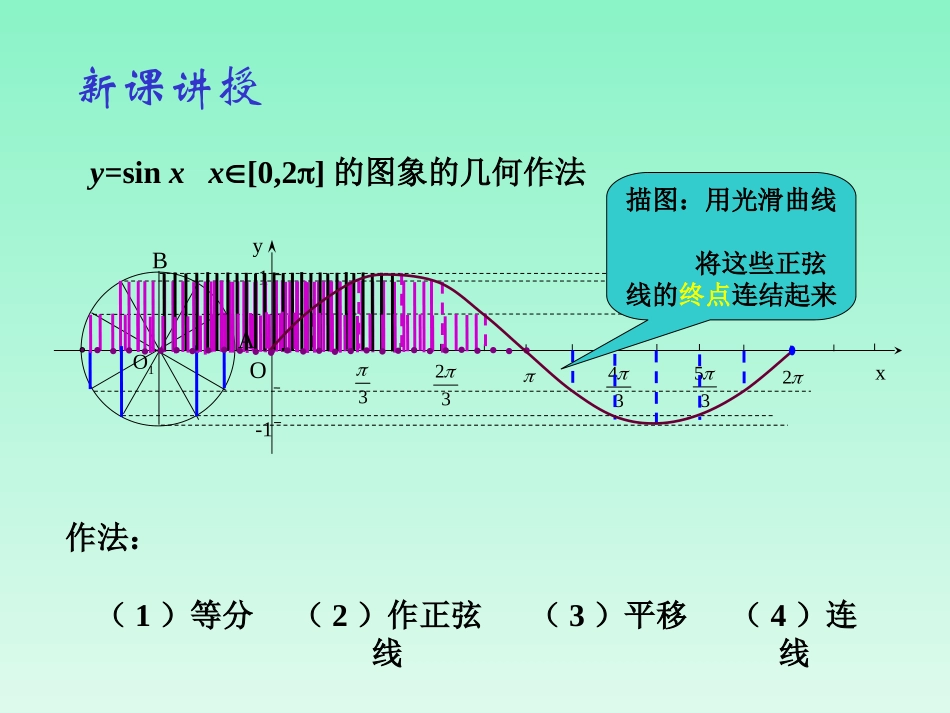
正弦函数、余弦函数的图象X肃宁一中李秋芳y=sinxx[0,2]的图象的几何作法O1Oyx33234352-11描图：用光滑曲线将这些正弦线的终点连结起来AB作法：（1）等分（2）作正弦线（3）平移（4）连线新课讲授yxo1-122322在作出正弦函数的图象时，应抓住哪些关键点？(0,0)(,1)2(,0)(,-1)23(2,0)如何作出y=sinx，xR∈的图象？思考：根据正弦函数“周而复始”的变化规律，如何作出[2,4][4,6][-2,0]上y=sinx的图象x6yo--12345-2-3-41正弦曲线探究：你能根据诱导公式，以正弦函数的图象为基础，通过适当的图形变换得到余弦函数y=cosx的图象吗？提示：由诱导公式六，我们有y=cosx=sin(+x)，xR∈，即y=cosx的图象就是y=sin(+x)的图象。22x6yo--12345-2-3-41余弦函数的图象正弦函数的图象x6yo--12345-2-3-41y=cosx=sin(x+),xR2余弦曲线正弦曲线形状完全一样只是位置不同正弦曲线、余弦曲线的特征：（1）图象为光滑的曲线，形如横“S”型的连接（2）图象每隔2π都会重复出现（3）图象是夹在y=1与y=-1之间的曲线yxo1-122322找出余弦函数y=cosx，x∈【0，2π】图象的五个关键点？(0,1)(,0)2(,-1)(,0)23(2,1)五点法——(0,1)(,0)2(,-1)(,0)23(2,1)探究：例1画出函数y=1+sinx，x[0,2]的简图：xsinx1+sinx22302010-101o1yx22322-12y=sinx，x[0,2]y=1+sinx，x[0,2]步骤：1.列表2.描点3.连线解：按五个关键点列表：描点并将它们用光滑曲线连接起来：1210例2画出函数y=-cosx，x[0,2]的简图：xcosx-cosx2230210-101-1yxo1-122322y=-cosx，x[0,2]y=cosx，x[0,2]解：按五个关键点列表：描点并将它们用光滑曲线连接起来：-1010当堂小测2.用“五点法”作出函数y＝-1－cosx(0≤x≤2π)的简图.1.用“五点法”作出函数y＝2sinx(0≤x≤2π)的简图.1.用五点法画的图象的步骤：2.用“五点法”画的正弦型函数在一个周期[0，2π]内的图象，如果要画出在其他区间上的图象，可依据图象的变化趋势和周期性画出.小结再见