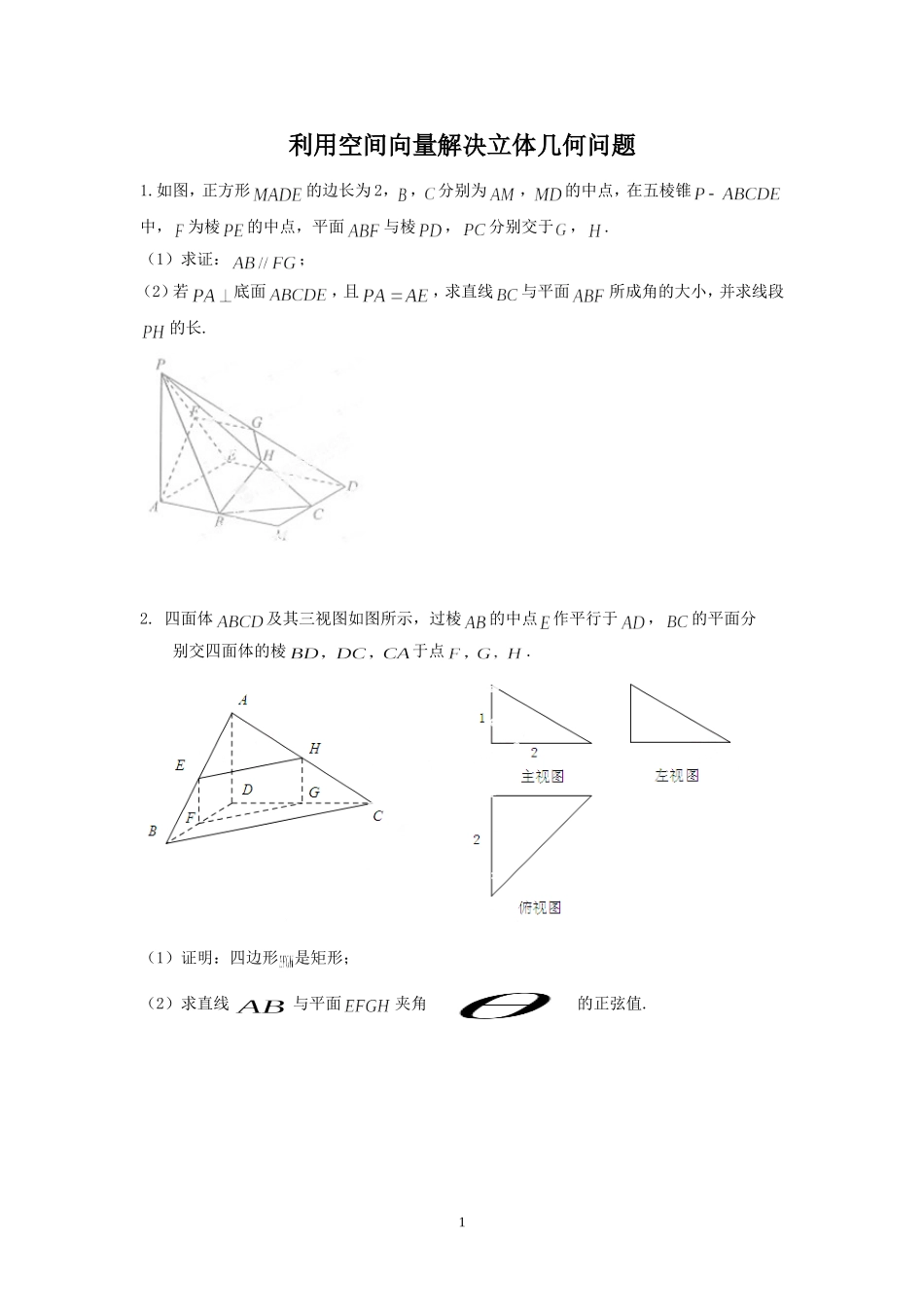
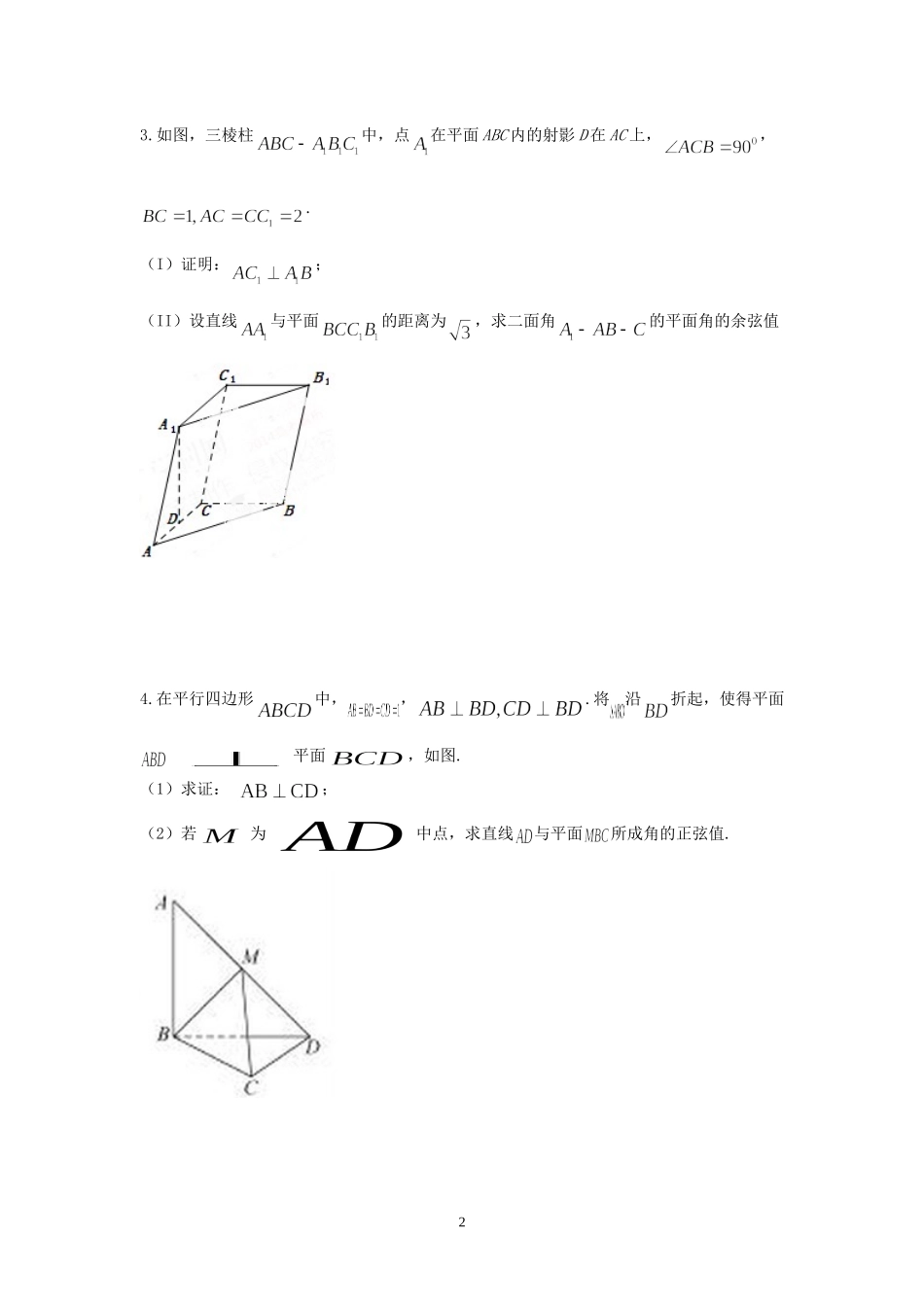
利用空间向量解决立体几何问题1.如图,正方形的边长为2,,分别为,的中点,在五棱锥中,为棱的中点,平面与棱,分别交于,.(1)求证:;(2)若底面,且,求直线与平面所成角的大小,并求线段的长.2.四面体及其三视图如图所示,过棱的中点作平行于,的平面分别交四面体的棱于点.(1)证明:四边形是矩形;(2)求直线与平面夹角的正弦值.13.如图,三棱柱中,点在平面ABC内的射影D在AC上,,.(I)证明:;(II)设直线与平面的距离为,求二面角的平面角的余弦值4.在平行四边形中,,.将沿折起,使得平面平面,如图.(1)求证:;(2)若为中点,求直线与平面所成角的正弦值.25.如图,四边形为正方形,平面,,于点,,交于点.(1)证明:;(2)求二面角的余弦值.6.如图,在棱长为2的正方体中,分别是棱的中点,点分别在棱,上移动,且.(1)当时,证明:直线平面;(2)是否存在,使平面与面所成的二面角为直二面角?若存在,求出的值;若不存在,说明理由.37.如图,四棱柱的所有棱长都相等,,四边形和四边形为矩形.(1)证明:底面;(2)若,求二面角的余弦值.8.如图,四棱锥中,为矩形,平面平面.(1)求证:(2)若问为何值时,四棱锥的体积最大?并求此时平面与平面夹角的余弦值.[来源:Z#xx#k.Com]49.如图,和所在平面互相垂直,且,,E、F分别为AC、DC的中点.(1)求证:;(2)求二面角的正弦值.10.如图,三棱柱中,侧面为菱形,.(Ⅰ)证明:;(Ⅱ)若,,,求二面角的余弦值.511.如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.(Ⅰ)证明:PB∥平面AEC;(Ⅱ)设二面角D-AE-C为60°,AP=1,AD=,求三棱锥E-ACD的体积.12.如图,在四棱柱中,底面是等腰梯形,,,是线段的中点.(Ⅰ)求证:;(Ⅱ)若垂直于平面且,求平面和平面所成的角(锐角)的余弦值.613.如图,四棱柱中,底面.四边形为梯形,,且.过三点的平面记为,与的交点为.(1)证明:为的中点;(2)求此四棱柱被平面所分成上下两部分的体积之比;(3)若,,梯形的面积为6,求平面与底面所成二面角大小.14.三棱锥ABCD及其侧视图、俯视图如图所示.设M,N分别为线段AD,AB的中点,P为线段BC上的点,且MNNP.(1)证明:P为线段BC的中点;(2)求二面角ANPM的余弦值.715.如图,在四棱锥中,底面,,,,,点为棱的中点.(Ⅰ)证明:;(Ⅱ)求直线与平面所成角的正弦值;(Ⅲ)若为棱上一点,满足,求二面角的余弦值.16.如图,在四棱锥中,平面平面.(1)证明:平面;8zyxPEDCBA(2)求二面角的大小EDCBA17.如图,四棱锥中,底面是以为中心的菱形,底面,,为上一点,且.(Ⅰ)求的长;(Ⅱ)求二面角的正弦值.18.在四棱锥中,底面是边长为1的菱形,,,,为的中点,为的中点(1)证明:;(2)求异面直线与所成角的大小;(3)求点到平面的距离.919.在四棱锥中,侧面,,底面为直角梯形,其中,,为中点.(1)求证:;(2)求异面直线与所成角余弦值;(3)求点到平面的距离.20.平面,是以为斜边的等腰直角三角形,分别是中点,(1)设是中点,证明:;(2)证明:在内存在一点,使得,并求出到的距离10