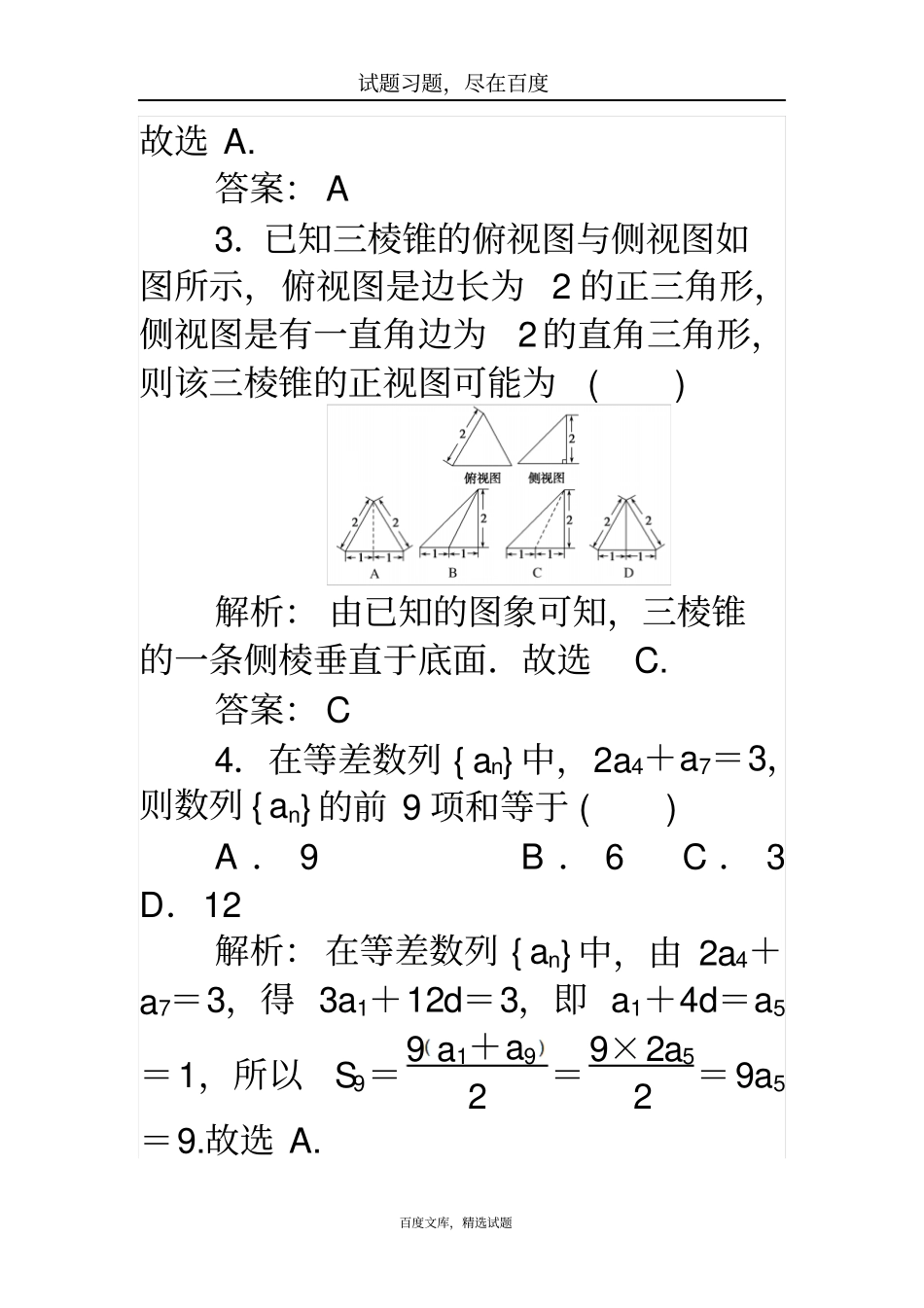
试题习题,尽在百度百度文库,精选试题高考小题标准练(十一)小题强化练,练就速度和技能,掌握高考得分点!姓名:________班级:________一、选择题(本大题共10小题,每小5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设全集U={1,2,3,4,5},集合A={1,2},B={2,3,5},则(?UA)∪B=()A.{3,5}B.{3,4,5}C.{2,3,4,5}D.{1,2,3,4}解析:因为全集U={1,2,3,4,5},A={1,2},所以?UA={3,4,5},所以(?UA)∪B={2,3,4,5}.故选C.答案:C2.已知(1+i)z=2i,则复数z=()A.1+iB.1-iC.-1+iD.-1-i解析:由z=2i1+i=2i1-i2=i+1.试题习题,尽在百度百度文库,精选试题故选A.答案:A3.已知三棱锥的俯视图与侧视图如图所示,俯视图是边长为2的正三角形,侧视图是有一直角边为2的直角三角形,则该三棱锥的正视图可能为()解析:由已知的图象可知,三棱锥的一条侧棱垂直于底面.故选C.答案:C4.在等差数列{an}中,2a4+a7=3,则数列{an}的前9项和等于()A.9B.6C.3D.12解析:在等差数列{an}中,由2a4+a7=3,得3a1+12d=3,即a1+4d=a5=1,所以S9=9a1+a92=9×2a52=9a5=9.故选A.试题习题,尽在百度百度文库,精选试题答案:A5.设x,y均为正实数,且12+x+12+y=13,则xy的最小值为()A.0B.4C.8D.16解析:因为x,y均为正实数,且12+x+12+y=13,进一步化简得xy-x-y-8=0,即x+y=xy-8≥2xy,令t=xy,t2-2t-8≥0,所以t≤-2(舍去)或t≥4,即xy≥4,化简可得xy≥16,所以xy的最小值为16.故选D.答案:D6.已知⊙A1:(x+2)2+y2=12和点A2(2,0),则过点A2且与⊙A1相切的动圆圆心P的轨迹方程为()A.x23-y2=1B.x23+y2=1C.x2-y2=2D.x212+y28=1试题习题,尽在百度百度文库,精选试题解析:根据题意有||PA1|-|PA2||=23<|A1A2|=4,所以点P的轨迹是以A1(-2,0),A2(2,0)为焦点,实轴长为2a=23的双曲线,可得b2=c2-a2=1,所以求得的轨迹方程为x23-y2=1.故选A.答案:A7.已知x+ax6(a>0)的展开式中常数项为240,则(x+a)(x-2a)2的展开式中x2项的系数为()A.10B.-8C.-6D.4解析:x+ax6的展开式中,常数项为C46x2ax4=15a4=240,则a4=16,解得a=2,(x+a)(x-2a)2的展开式中,x2项为x·C12x·(-2a)+a·x2=-3ax2,则x2项的系数为-6.故选C.答案:C8.已知△ABC的外接圆的圆心为试题习题,尽在百度百度文库,精选试题O,半径为2,OA→+AB→+AC→=0且|OA→|=|AB→|,则向量CA→在CB→方向上的投影为()A.3B.3C.-3D.-3解析:因为OA→+AB→+AC→=0,所以OB→=CA→,所以四边形OBAC为平行四边形.又|OA→|=|AB→|,所以△OAB与△OAC均为等边三角形,所以∠ACB=30°,所以向量CA→在CB→方向上的投影为|CA→|cos30°=2×32=3.故选A.答案:A9.下列说法中,错误的是()A.已知a,b,m∈R,命题“若am2
0”的否定是“?x∈R,x2-x≤0”C.命题“p或q”为真命题,则命试题习题,尽在百度百度文库,精选试题题p和q均为真命题D.“x>3”是“x>2”的充分不必要条件解析:若am20,则a3可得x>2,而x>2无法推出x>3,故D正确.故选C.答案:C10.已知a>0,且a≠1,则函数f(x)=ax+(x-1)2-2a的零点个数为()A.1B.2C.3D.与a有关解析:由f(x)=ax+(x-1)2-2a=0,得ax=-(x-1)2+2a,设y1=ax,这是一个指数函数,y2=-(x-1)2+2a,这是一个二次函数,其对称轴为x=1,开口向下,最大值为2a,与y轴交点的纵坐标为2a-1,当a>1时,作出两个函数的图象(如图1),显然此时两个函数的图象有两个交点,即函数f(x)有两个零点;当试题习题,尽在百度百度文库,精选试题0