北京第十八中学高三数学第一轮复习 51 平面向量的数量积（或内积）教学案（教师版）VIP免费

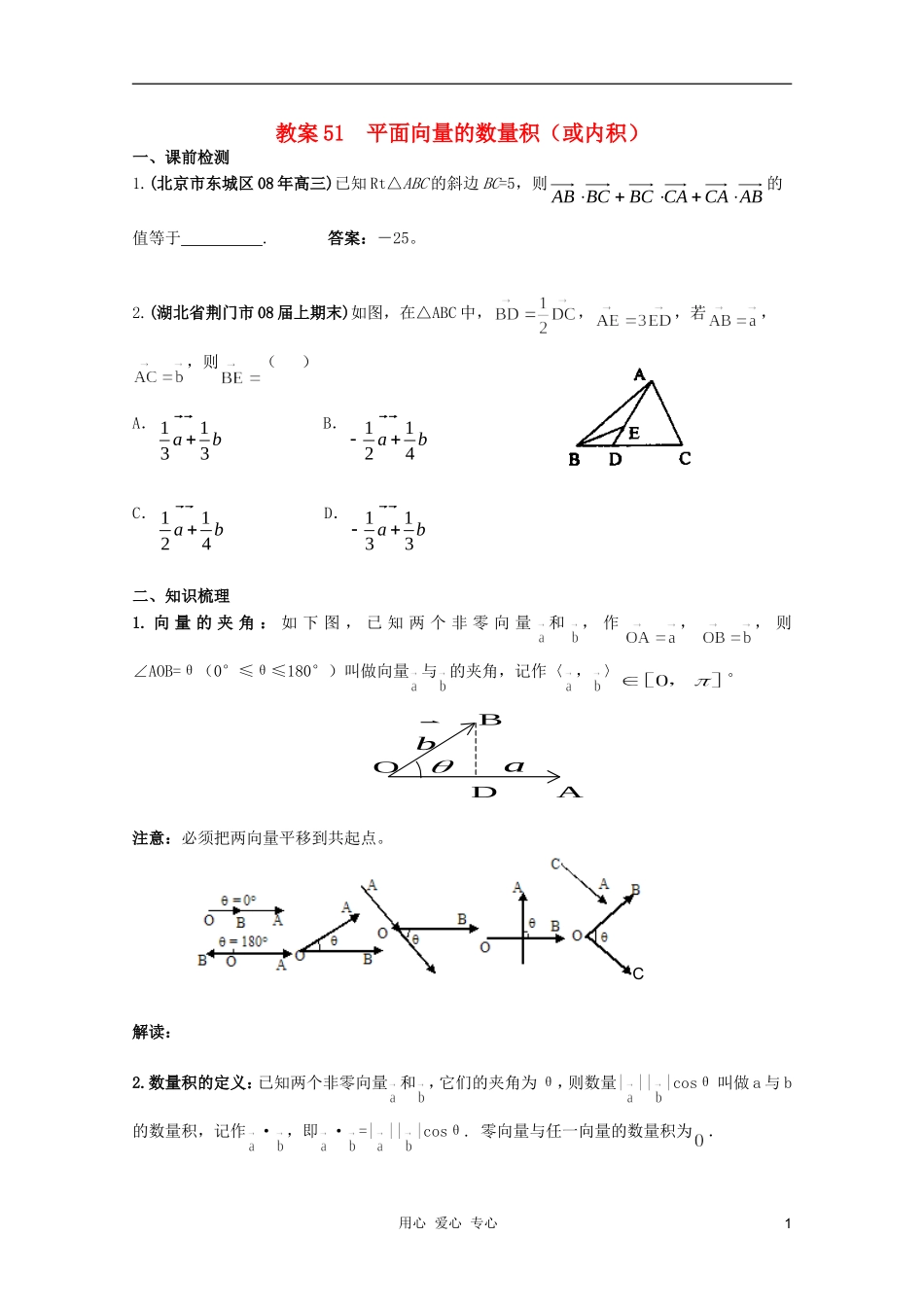
教案51平面向量的数量积（或内积）一、课前检测1.(北京市东城区08年高三)已知Rt△ABC的斜边BC=5，则ABCACABCBCAB的值等于.答案：－25。2.(湖北省荆门市08届上期末)如图，在△ABC中，，，若，，则（）A．1133abB．1124abC．1124abD．1133ab二、知识梳理1.向量的夹角：如下图，已知两个非零向量和，作，，则∠AOB=θ（0°≤θ≤180°）叫做向量与的夹角，记作〈，〉。BbODAa注意：必须把两向量平移到共起点。解读：2.数量积的定义：已知两个非零向量和，它们的夹角为θ，则数量||||cosθ叫做a与b的数量积，记作·，即·=||||cosθ.零向量与任一向量的数量积为．用心爱心专心1C注意：，，。解读：3.数量积的几何意义：①||cos〈，〉叫做在方向上的投影；||cos〈，〉叫做在方向上的投影；②·的几何意义：·等于||与在方向上的投影||cos〈，〉乘积或等于||与在方向上的投影||cos〈，〉乘积。解读：4.数量积的性质：设是单位向量，〈，〉=θ.1）·=·=||cosθ.与同向的单位向量的求法：。平行的单位向量呢？2）在方向上的投影为：；在方向上的投影︱b︱cos=||aba∈R。3）当与同向时，·=||||；当与反向时，·=－||||，特别地，·=||2，或||=.4）.5）6）.7）cosθ=.①为锐角,不同向；为直角；为钝角,不反向.②∥··或··ababababab||||||||abb（，惟一确定）08）|·|≤||||.解读：用心爱心专心25.数量积的运算法则（运算律）①··abba；②③（λ）·=λ（·）=·（λ）注意：1）数量积不满足结合律2）已知向量ABa�和轴l，e是l上与l同方向的单位向量，作点A在l上的射影A，作点B在l上的射影B，则AB�叫做向量AB�在轴l上或在e上的正射影.可以证明AB�的长度||||cos,||ABABaeae�．3）数量积的物理意义——力作功：一个物体在力的作用下产生位移，那么力所作的功，其中是与的夹角，从而.解读：三、典型例题分析例1已知|a|＝4，|b|＝5，且a与b的夹角为60°，求：(2a＋3b)·(3a－2b)．解:(2a＋3b)(3a－2b)＝－4变式训练1已知|a|＝3，|b|＝4，|a＋b|＝5，求|2a－3b|的值．解:56变式训练2若向量a与b的夹角为60°，|b|=4，（a+2b）·（a－3b）=－72，则向量a的模是（C）A.2B.4C.6D.12解析：（a+2b）·（a－3b）=|a|2－|a||b|cos60°－6|b|2=|a|2－2|a|－96=－72，∴|a|2－2|a|－24=0.∴（|a|－6）·（|a|+4）=0.∴|a|=6.小结与拓展：例2如图，在等腰直角ΔABC中，∠C=90°，|AB|=2.求（1）的值；（2）的值；（3）用心爱心专心3变式训练3在中,,则的值为()A.20B.C.D.答案:B变式训练4已知为（C）A.锐角三角形B.直角三角形C.钝角三角形D.不能确定小结与拓展：例3已知||=，||=3，和夹角为450，求当向量+λ与λ+夹角为锐角时，λ的取值范围。答案：λ<，或λ>且λ≠1变式训练5已知|a|=10，|b|=12，且（3a）·（b）=－36，则a与b的夹角是（B）A.60°B.120°C.135°D.150°解析：由（3a）·（b）=－36得a·b=－60.∴cos〈a，b〉==－.又0°≤〈a，b〉≤180°，∴〈a，b〉=120°.变式训练6.若向量c垂直于向量a和b，d=λa+μb（λ、μ∈R，且λμ≠0），则（B）A.c∥dB.c⊥dC.c不平行于d，也不垂直于dD.以上三种情况均有可能解析：∵c⊥a，c⊥b，∴c·a=0，c·b=0.∴c·d=c·（λa+μb）=c·（λa）+c·（μb）=λc·a+μc·b=0.小结与拓展：四、归纳与总结（以学生为主，师生共同完成）1.知识：2.思想与方法：3.易错点：用心爱心专心44.教学反思（不足并查漏）用心爱心专心5