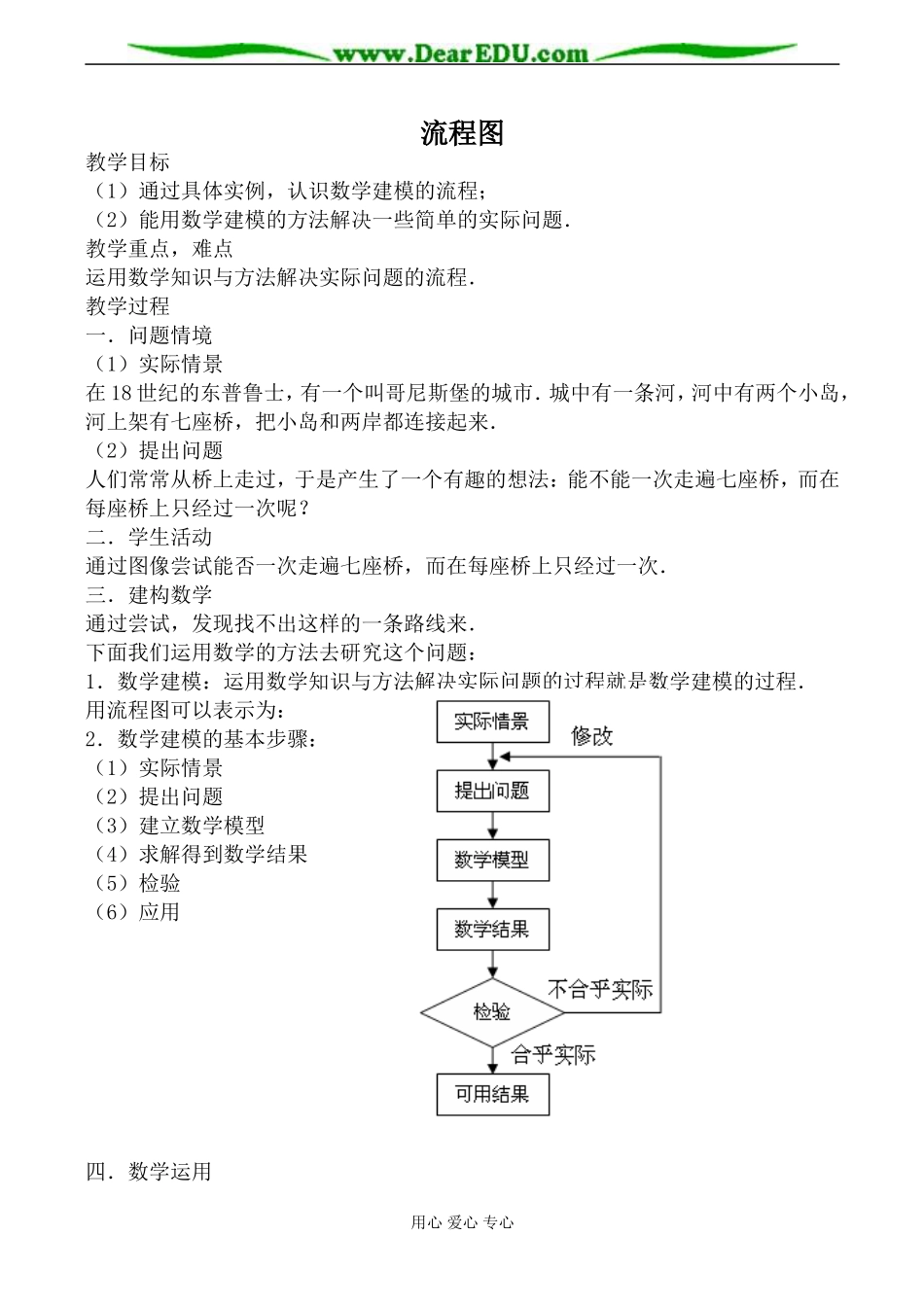
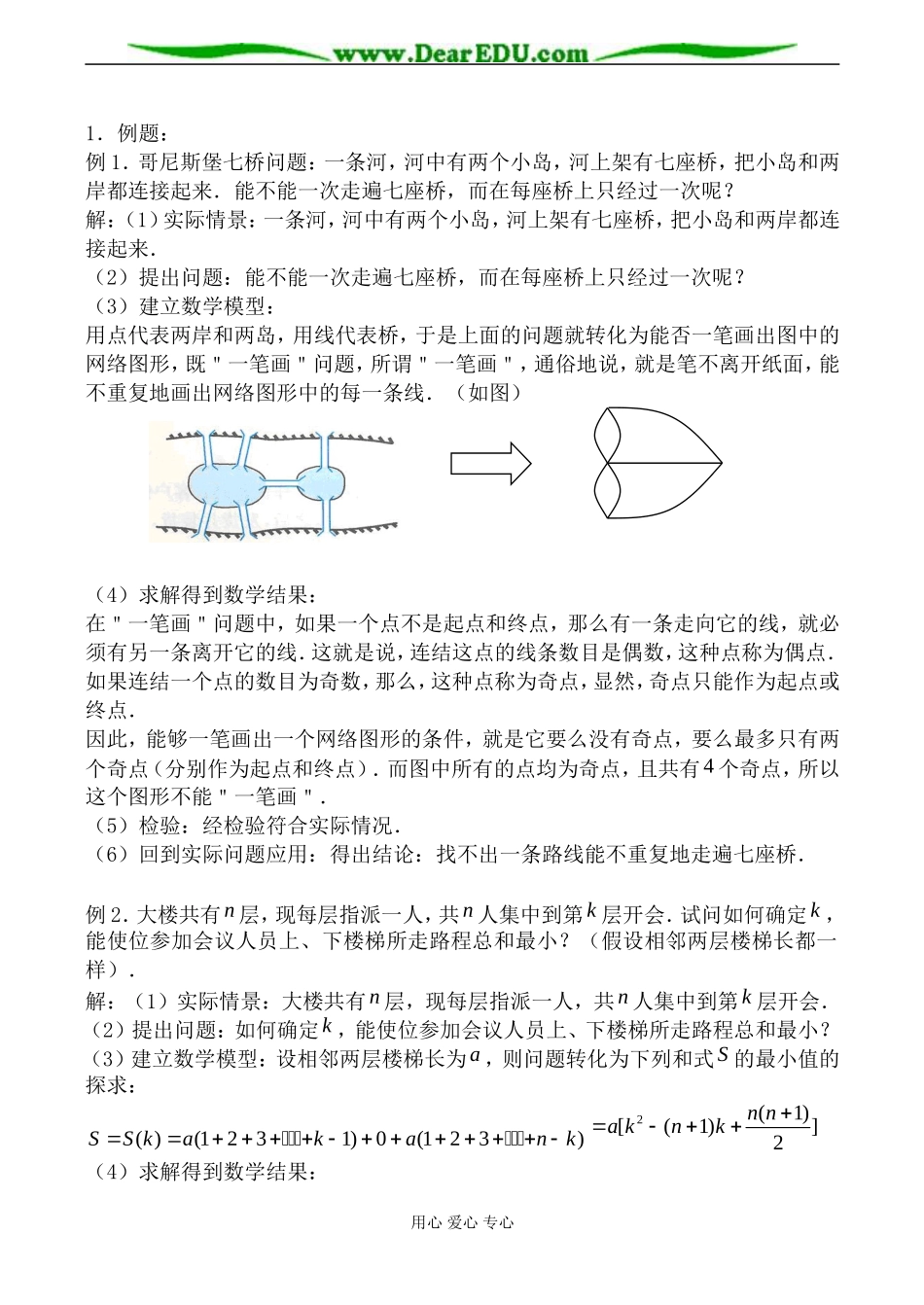
流程图教学目标(1)通过具体实例,认识数学建模的流程;(2)能用数学建模的方法解决一些简单的实际问题.教学重点,难点运用数学知识与方法解决实际问题的流程.教学过程一.问题情境(1)实际情景在18世纪的东普鲁士,有一个叫哥尼斯堡的城市.城中有一条河,河中有两个小岛,河上架有七座桥,把小岛和两岸都连接起来.(2)提出问题人们常常从桥上走过,于是产生了一个有趣的想法:能不能一次走遍七座桥,而在每座桥上只经过一次呢?二.学生活动通过图像尝试能否一次走遍七座桥,而在每座桥上只经过一次.三.建构数学通过尝试,发现找不出这样的一条路线来.下面我们运用数学的方法去研究这个问题:1.数学建模:运用数学知识与方法解决实际问题的过程就是数学建模的过程.用流程图可以表示为:2.数学建模的基本步骤:(1)实际情景(2)提出问题(3)建立数学模型(4)求解得到数学结果(5)检验(6)应用四.数学运用用心爱心专心1.例题:例1.哥尼斯堡七桥问题:一条河,河中有两个小岛,河上架有七座桥,把小岛和两岸都连接起来.能不能一次走遍七座桥,而在每座桥上只经过一次呢?解:(1)实际情景:一条河,河中有两个小岛,河上架有七座桥,把小岛和两岸都连接起来.(2)提出问题:能不能一次走遍七座桥,而在每座桥上只经过一次呢?(3)建立数学模型:用点代表两岸和两岛,用线代表桥,于是上面的问题就转化为能否一笔画出图中的网络图形,既"一笔画"问题,所谓"一笔画",通俗地说,就是笔不离开纸面,能不重复地画出网络图形中的每一条线.(如图)(4)求解得到数学结果:在"一笔画"问题中,如果一个点不是起点和终点,那么有一条走向它的线,就必须有另一条离开它的线.这就是说,连结这点的线条数目是偶数,这种点称为偶点.如果连结一个点的数目为奇数,那么,这种点称为奇点,显然,奇点只能作为起点或终点.因此,能够一笔画出一个网络图形的条件,就是它要么没有奇点,要么最多只有两个奇点(分别作为起点和终点).而图中所有的点均为奇点,且共有4个奇点,所以这个图形不能"一笔画".(5)检验:经检验符合实际情况.(6)回到实际问题应用:得出结论:找不出一条路线能不重复地走遍七座桥.例2.大楼共有n层,现每层指派一人,共n人集中到第k层开会.试问如何确定k,能使位参加会议人员上、下楼梯所走路程总和最小?(假设相邻两层楼梯长都一样).解:(1)实际情景:大楼共有n层,现每层指派一人,共n人集中到第k层开会.(2)提出问题:如何确定k,能使位参加会议人员上、下楼梯所走路程总和最小?(3)建立数学模型:设相邻两层楼梯长为a,则问题转化为下列和式S的最小值的探求:()(1231)0(123)SSkakank2(1)[(1)]2nnaknk(4)求解得到数学结果:用心爱心专心函数()Sk为k的二次函数,且0a,故当n为奇数时,取12nk,S最小;当为n偶数时,取2nk或12n,S最小.(5)检验:经检验符合实际情况.(6)回到实际问题应用:得出结论:故当层数n为奇数时,取12nk,路程总和最小;当层数n为偶数时,取2nk或12n,路程总和最小,即在楼的中间那层路程总和最小.五.回顾小结:1.数学建模的基本步骤,及流程图.六.课外作业:补充:1.试设计出解不等式0axb(0)a的流程图.2.已知函数5,1000,()(10),1000,xxfxfxx画出求(65)f的流程图.用心爱心专心