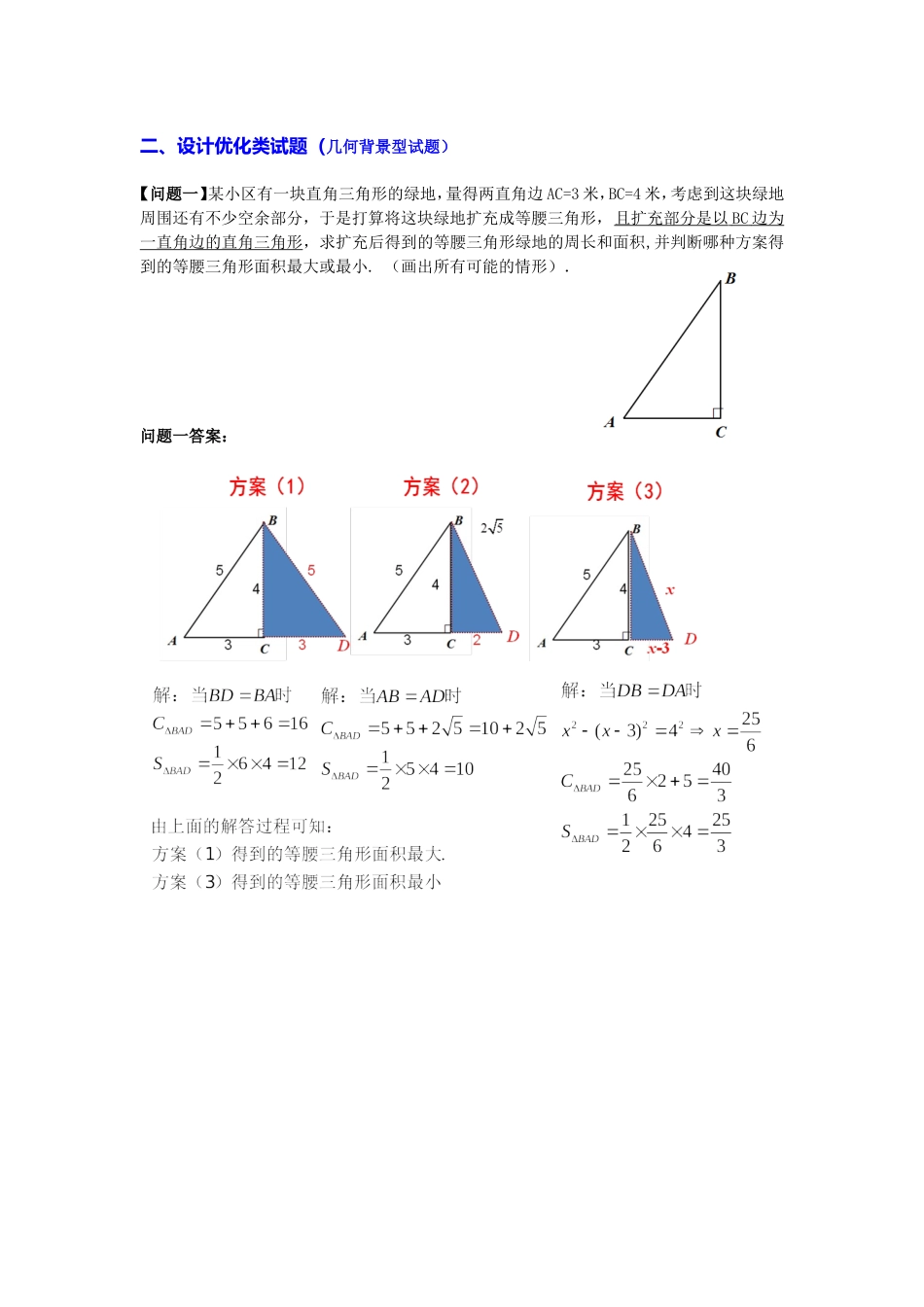
二、设计优化类试题(几何背景型试题)【问题一】某小区有一块直角三角形的绿地,量得两直角边AC=3米,BC=4米,考虑到这块绿地周围还有不少空余部分,于是打算将这块绿地扩充成等腰三角形,且扩充部分是以BC边为一直角边的直角三角形,求扩充后得到的等腰三角形绿地的周长和面积,并判断哪种方案得到的等腰三角形面积最大或最小.(画出所有可能的情形).问题一答案:【问题二】如图,要在一块形状为直角三角形的铁皮上裁出一个半圆形的铁皮,要求:①半圆形铁皮的直径在直角三角形的边上.②每一种裁剪的方案都要使剪下来的半圆形铁皮的面积尽可能的大.(1)请你用直尺和圆规作出该半圆;(要求保留作图痕迹,不要求写作法)(2)若BC=4m,AC=3m,求(1)中所画半圆的半径,并判断哪一种裁剪方案剪下来的半圆形铁皮面积最大.问题二答案:,=r=3-r3==4543ODOODAOADOACBODAOrrCBABr解:连结得∽设的半径则由,=r=4-r4==3532ODODBOBDOBCAODBOrrCAABOr解:连结设的半径则得∽由【问题三】已知:直角三角形的铁片ABC的两条直角边BC、AC的长分别为6cm和8cm,如图所示,分别采用(1)(2)两种方法,加工出一块正方形铁片,为使加工出的正方形面积最大,试比较哪种加工方法较为合理,并说明理由.【变式】已知:直角三角形的铁片ABC的两条直角边BC、AC的长分别为6cm和8cm,如图所示,分别采用(3)(4)两种方法,剪下边长为1cm的正方形铁片,为使剪下的正方形铁片块数最多,试比较哪种剪法较为合理,并说明理由。问题三答案:,,8868482401470CDEFDExADxDEADxxADEACBCBACx解:按照方案(1)加工出正方设正方形的形边则由∽得变式答案:1111111112233445566,7862149215439432AMMNMNAMNACBACBCMNMNMNMNMNMN由∽得第1层可以剪得5个小正方形同理:第2层可以剪得4个小正方形第3层可以剪得3个小正方形解:按照方案(3)第4层可以剪得3个小正方形第5层可以剪得2个小正方形第6层可以剪得1个小正方形按照方案(3)共可以剪得剪18个小正方形11223344,951235615453EFEFEFEF由相似三角形对应边上的高之比等于相似比第1层可以剪得7个小正方形同理:第2层可以剪得5个小正方形第3层可以剪得3个小正方形第4层解:可以剪得1个小正方形按照方案(4)共可以剪得按1照方案(4)剪6个小正方形.方案(3)剪由上面的解答过得的小正程知:方形最多可