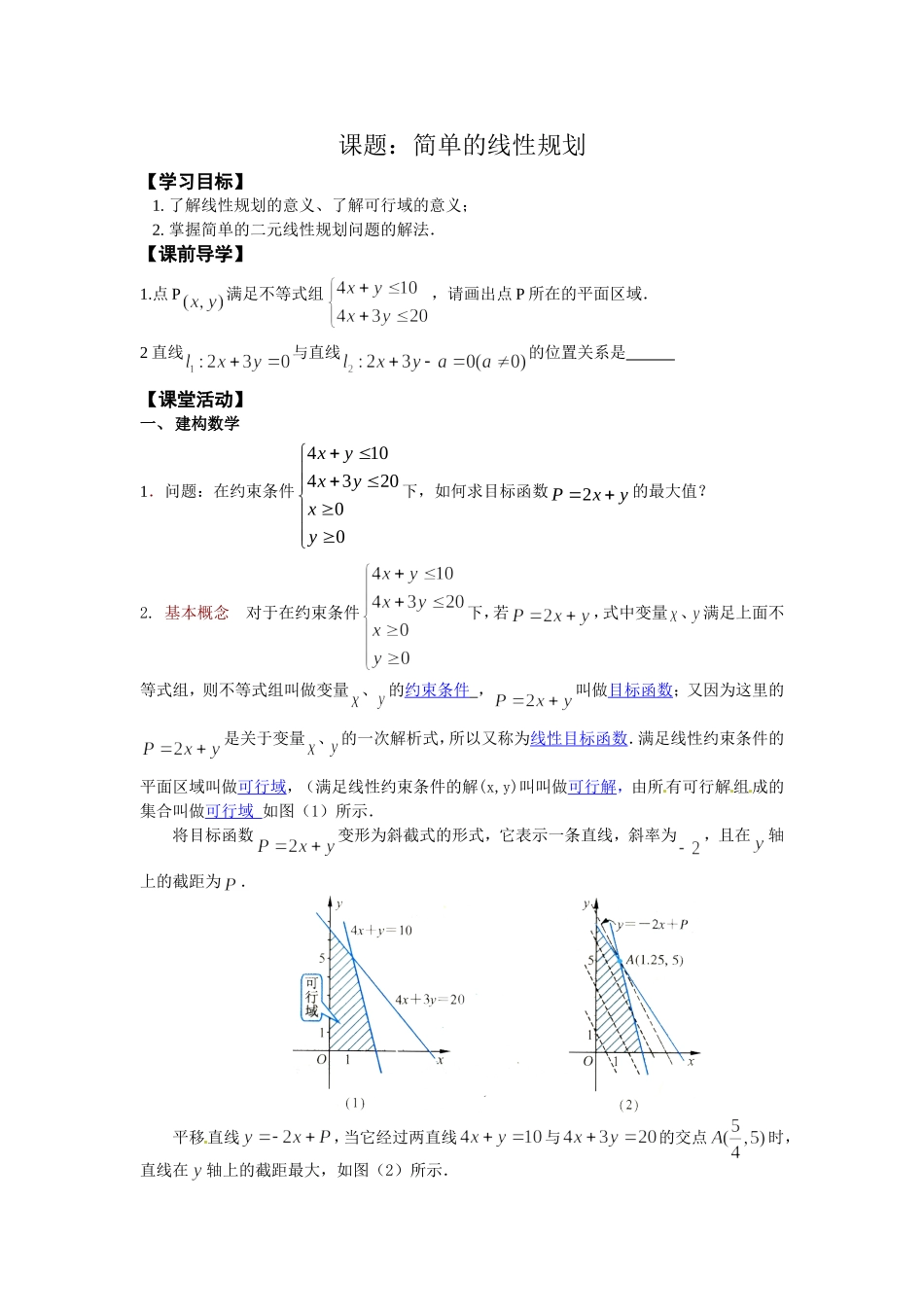
课题:简单的线性规划【学习目标】1.了解线性规划的意义、了解可行域的意义;2.掌握简单的二元线性规划问题的解法.【课前导学】1.点P满足不等式组,请画出点P所在的平面区域.2直线与直线的位置关系是【课堂活动】一、建构数学1.问题:在约束条件410432000xyxyxy下,如何求目标函数2Pxy的最大值?2.基本概念对于在约束条件下,若,式中变量、满足上面不等式组,则不等式组叫做变量、的约束条件,叫做目标函数;又因为这里的是关于变量、的一次解析式,所以又称为线性目标函数.满足线性约束条件的平面区域叫做可行域,(满足线性约束条件的解(x,y)叫叫做可行解,由所有可行解组成的集合叫做可行域如图(1)所示.将目标函数变形为斜截式的形式,它表示一条直线,斜率为,且在轴上的截距为.平移直线,当它经过两直线与的交点时,直线在轴上的截距最大,如图(2)所示.AbOBCD24420ab1ba4ba2baa因此,当时,目标函数取得最大值,即当甲、乙两种产品分别生产和时,可获得最大利润万元.这类求线性目标函数在线性约束条件下的最大值或最小值问题,通常称为线性规划问题.使目标函数取得最值,它叫做这个问题的最优解,本题中使目标函数取得最大值,它叫做这个问题的最优解.对于只含有两个变量的简单线性规划问题可用图解法来解决.[来源:Zxxk.Com]说明:平移直线时,要始终保持直线经过可行域(即直线与可行域有公共点).3.求解线性规划的最优解的步骤[来源:(1)列:设出未知数,列出约束条件,确定目标函数;(2)画:画出线性约束条件所表示的可行域;(3)移:在线性目标函数所表示的一组平行线中,利用平移的方法找出与可行域有公共点且纵截距最大或最小的直线;(4)求:通过解方程组求出最优解;(5)答:作出答案。变式练习变式1.在例1条件下,求P=2x+y+20的最大值与最小值变式2.在例1条件下,求P=2x-y的最大值与最小值变式3.在例1条件下,求P=4x+3y的最大值与最小值解:变式1:设:,平移类同例1,得P最大值为27.5,P最小值为20.变式2:设:,平移类同例1,得P最大值为5,P最小值为.变式3:设:,平移类同例1,得P最大值为20,P最小值为0.4.例1(1)已知1224abab,求42tab的取值范围;(2)设2()fxaxbx,且1(1)2f,2(1)4f,求(2)f的取值范围.【思路分析】先画出可行域,再平移直线即可.【解】(1)不等式组表示的平面区域如图所示,作直线:,作一组平行线:,由图知由向右下方平移时,随之增大,反之减小,∴当经过点时取最小值,当经过点时取最大值,由和分别得,,∴,,所以,.(2),,,由(1)知,.【解后反思】本题还可以借助不等式的性质求解.设,求出m,n.例2设2zxy,式中变量,xy满足条件4335251xyxyx,求z的最大值和最小值【思路分析】按照解决线性规划问题的步骤逐一实施:画出可行域——目标函数变形——平移直线——找出最优解.【解】由题意,变量所满足的每个不等式都表示一个平面区域,不等式组则表示这些平面区域的公共区域.由图知,原点不在公共区域内,当时,,即点在直线:上,作一组平行于的直线:,,可知:当在的右上方时,直线上的点满足,即,而且,直线往右平移时,随之增大.[来源:Z§xx§k.Com]由图象可知,当直线经过点时,对应的最大,当直线经过点时,对应的最小,所以,,.【变题】设,式中满足条件,求的最大值和最小值.解:由引例可知:直线与所在直线平行,则由引例的解题过程知,当与所在直线重合时最大,此时满足条件的最优解有无数多个,当经过点时,对应最小,∴,.【解后反思】(1)线性目标函数的最大值、最小值一般在可行域的顶点处取得;(2)线性目标函数的最大值、最小值也可在可行域的边界上取得,即满足条件的最优解有无数多个.例3求54zxy的最大值,使式中,xy满足约束条件321041100,0,xyxyxyxyZ.【思路分析】先画出可行域中的网格,找出整点,再去平移直线.注意平移直线时,只能经过整点.【解】先画出可行域中的网格,...