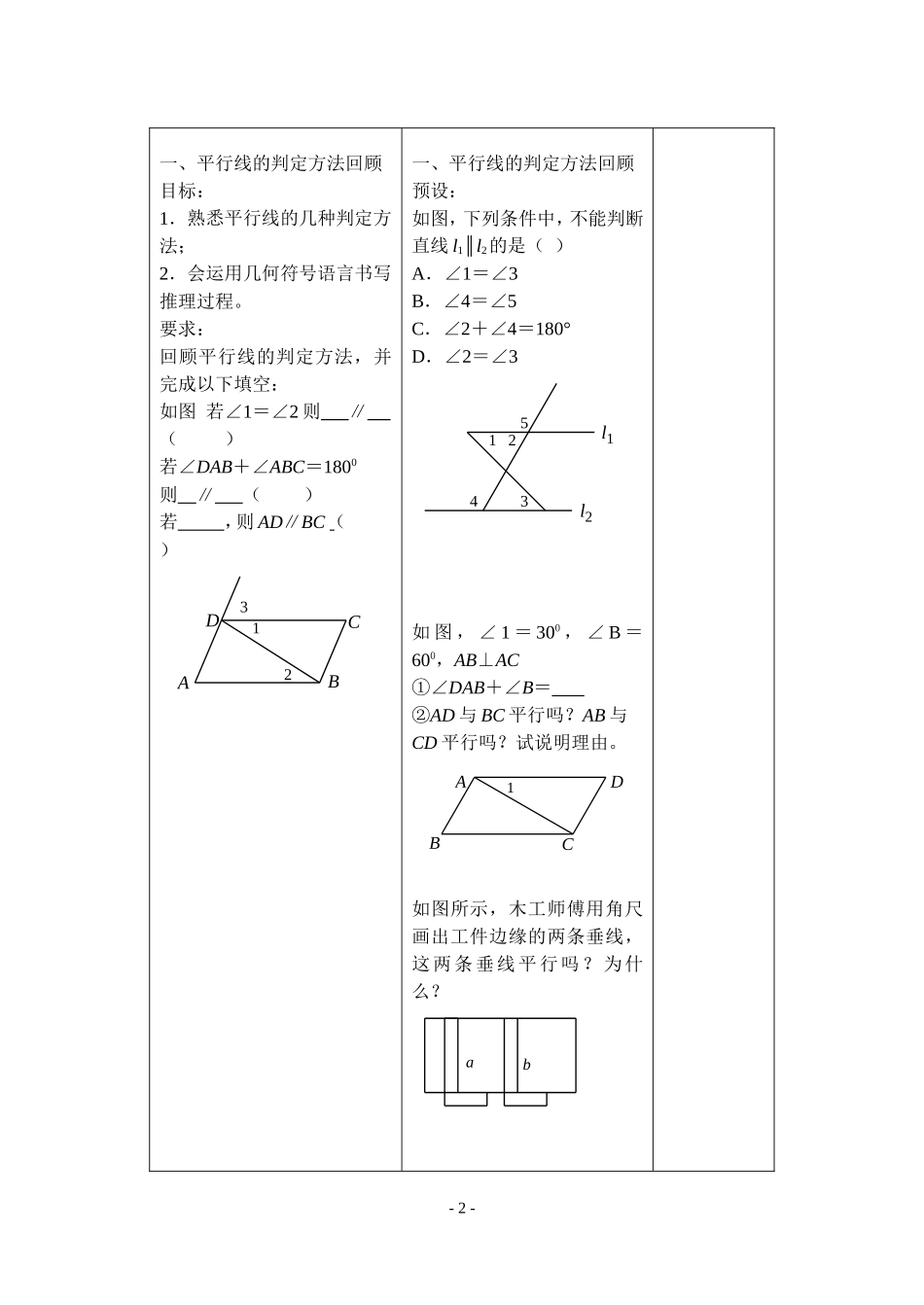
平行线的判定课时教学计划海门市悦来初级中学茅永华学程设计导学策略调整与反思-1-教学内容平行线的判定共几课时课型第几课时1教学目标1.能够根据题意,灵活选用合适的方法判定两条直线平行;2.在选用合适的判定方法判定直线平行的过程中,体会一题多解,养成题后反思的习惯;3.学习几何证明推理的书写教学重难点重点:1.选用合适的方法判定两直线平行2.几何证明推理的书写难点:1.根据问题情况选择最好的方法;2.几何证明推理的书写教学资源学生已经认识了平行线的几种判定方法板书设计一、平行线的判定方法回顾目标:1.熟悉平行线的几种判定方法;2.会运用几何符号语言书写推理过程。要求:回顾平行线的判定方法,并完成以下填空:如图若∠1=∠2则∥()若∠DAB+∠ABC=1800则∥()若,则AD∥BC()DCBA321一、平行线的判定方法回顾预设:如图,下列条件中,不能判断直线l1∥l2的是()A.∠1=∠3B.∠4=∠5C.∠2+∠4=180°D.∠2=∠3l2l154321如图,∠1=300,∠B=600,AB⊥AC①∠DAB+∠B=②AD与BC平行吗?AB与CD平行吗?试说明理由。DCBA1如图所示,木工师傅用角尺画出工件边缘的两条垂线,这两条垂线平行吗?为什么?ba-2-学程设计导学策略调整与反思-3-若a⊥b,c⊥b则a与c的关系是()A.平行B.垂直C.相交D.以上都不对已知:如图,CD⊥DA,DA⊥AB,∠1=∠2,试确定射线DF与AE的位置关系,并说明你的理由.(1)问题的结论:DF_____AE.(2)证明思路分析:欲证DF___AE,只要证∠3=____.(3)证明过程:证明:∵CD⊥DA,DA⊥AB,()∴∠CDA=∠DAB=___°.(垂直定义)又∠1=∠2,()从而∠CDA-∠1=______-______,(等式的性质)即∠3=______.∴DF______AE.(______,___________)如图,ADB是一条直线,∠ADE=∠ABC且DG、BF分别是∠ADE和∠ABC的角平分线,那么DG一定平行于BF吗?为什么?如图BE是∠ABC的平分线,∠1=∠2说明DE∥BC的理由学程设计导学策略调整与反思-4-已知:如图,∠ABC=∠ADC,BF、DE分别平分∠ABC与∠ADC,且∠1=∠3.求证:AB∥DC.课堂小结:平行线的判定方法思考,讨论,寻找方法,展示思路,教师板书示范过程作业设计-5-