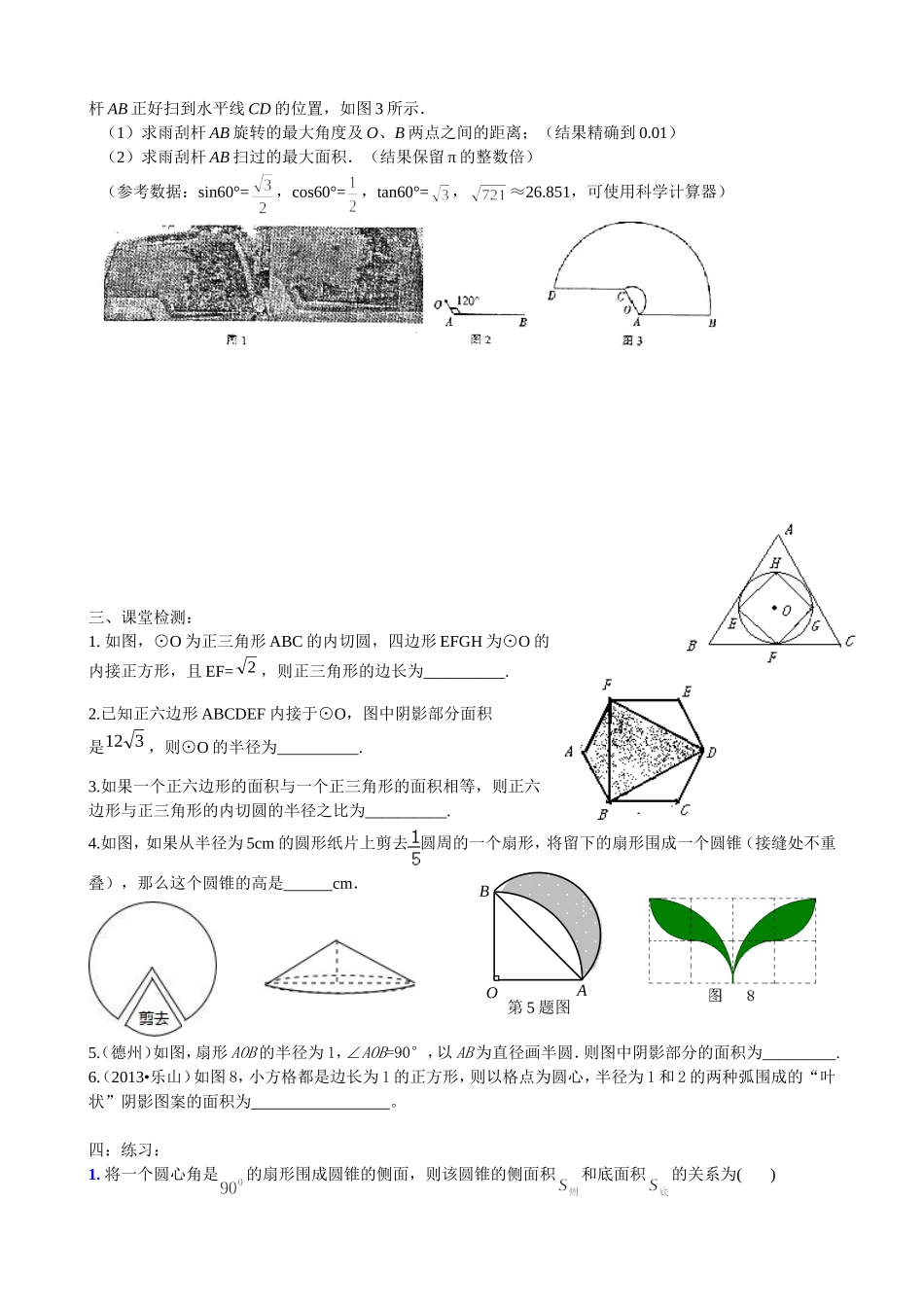
期末复习四:正多边形和圆,弧长和扇形面积一、基础练习:1、已知⊙O的半径为R,正六边形ABCDEF是⊙O的内接正六边形,则正六边形ABCDEF的周长是___________,面积___________.2、一个正多边形绕它的中心旋转36°后,才与原正多边形第一次重合,那么这个正多边形是.3、如图,已知⊙O的外切正六边形的半径为4,则该圆的内接正三角形的边心距是4、如图是一个滑轮起重装置,滑轮的半径是10cm,当重物上升10cm时,则滑轮的一条半径OA绕轴心O按逆时针方向转动的角度是5.圆心角为60°,且半径为3的扇形的弧长为6、如图,冰激凌蛋筒下部是圆锥形,蛋筒圆锥部分包纸的面积是.二、例题:1.如图,正方形OABC放在坡角为30°的坡面OM上,先将正方形OABC绕O点沿顺时针方向旋转到水平地面ON上的ODEF处,若正方形的边长为2cm,求旋转过程中点B运动的轨迹长.2.如图,在△ABC中,C=90°,AC=3,BC=4.将△ABC以直角边所在的直线为轴旋转一周,求所得旋转体的表面积。3.(绵阳2013)如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连接CE。(1)判断CD与⊙O的位置关系,并证明你的结论;(2)若E是的中点,⊙O的半径为1,求图中阴影部分的面积。4、(2013江西)如图1,一辆汽车的背面,有一种特殊形状的刮雨器,忽略刮雨器的宽度可抽象为一条折线OAB,如图2所示,量得连杆OA长为10cm,雨刮杆AB长为48cm,∠OAB=120°.若启动一次刮雨器,雨刮杆AB正好扫到水平线CD的位置,如图3所示.(1)求雨刮杆AB旋转的最大角度及O、B两点之间的距离;(结果精确到0.01)(2)求雨刮杆AB扫过的最大面积.(结果保留π的整数倍)(参考数据:sin60°=,cos60°=,tan60°=,≈26.851,可使用科学计算器)三、课堂检测:1.如图,⊙O为正三角形ABC的内切圆,四边形EFGH为⊙O的内接正方形,且EF=2,则正三角形的边长为__________.2.已知正六边形ABCDEF内接于⊙O,图中阴影部分面积是312,则⊙O的半径为__________.3.如果一个正六边形的面积与一个正三角形的面积相等,则正六边形与正三角形的内切圆的半径之比为__________.4.如图,如果从半径为5cm的圆形纸片上剪去圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高是cm.5.(德州)如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆.则图中阴影部分的面积为_________.6.(2013•乐山)如图8,小方格都是边长为1的正方形,则以格点为圆心,半径为1和2的两种弧围成的“叶状”阴影图案的面积为。四:练习:1.将一个圆心角是的扇形围成圆锥的侧面,则该圆锥的侧面积和底面积的关系为()OAB第5题图P'PB'A'NMBAO(第11题)A.=B.=2C.=3D.=42.小敏在作⊙O的内接正五边形时,先做了如下几个步骤:(1)作⊙O的两条互相垂直的直径,再作OA的垂直平分线交OA于点M,如图1;(2)以M为圆心,BM长为半径作圆弧,交CA于点D,连结BD,如图2.若⊙O的半径为1,则由以上作图得到的关于正五边形边长BD的等式是()A.BD2=ODB.BD2=ODC.BD2=ODD.BD2=OD3.如图,矩形ABCD中,AB=4,以点B为圆心,BA为半径画弧交BC于点E,以点O为圆心的⊙O与弧,边AD,DC都相切.把扇形BAE作一个圆锥的侧面,该圆锥的底面圆恰好是⊙O,则AD的长为()A.4B.C.112D.5(第3题)(第4题)(第5题)(第6题)4.如图所示,在直角坐标系中放置一个边长为1的正方形ABCD,将正方形ABCD沿x轴的正方向无滑动的在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径线与x轴围成的面积为.5.如图,△ABC是正三角形,曲线CDEF叫做正三角形的渐开线,其中弧CD、弧DE、弧EF的圆心依次是A、B、C,如果AB=1,那么曲线CDEF的长是.6.如图所示,一半径为1的圆内切于一个圆心角为60°的扇形,则扇形的周长为.(第7题)7.如图,正三角形ABC的边长是2,分别以点B,C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当≤r<2时,S的取值范围是.8.如图,是半圆的直径,且,点C为半圆上的一点.将此半圆沿所在的直线折叠,若圆弧恰好过圆心,则图中阴影部分的面积是.(结果保留)9.如图,一个半径为22的圆经过一个半径为4的圆的...