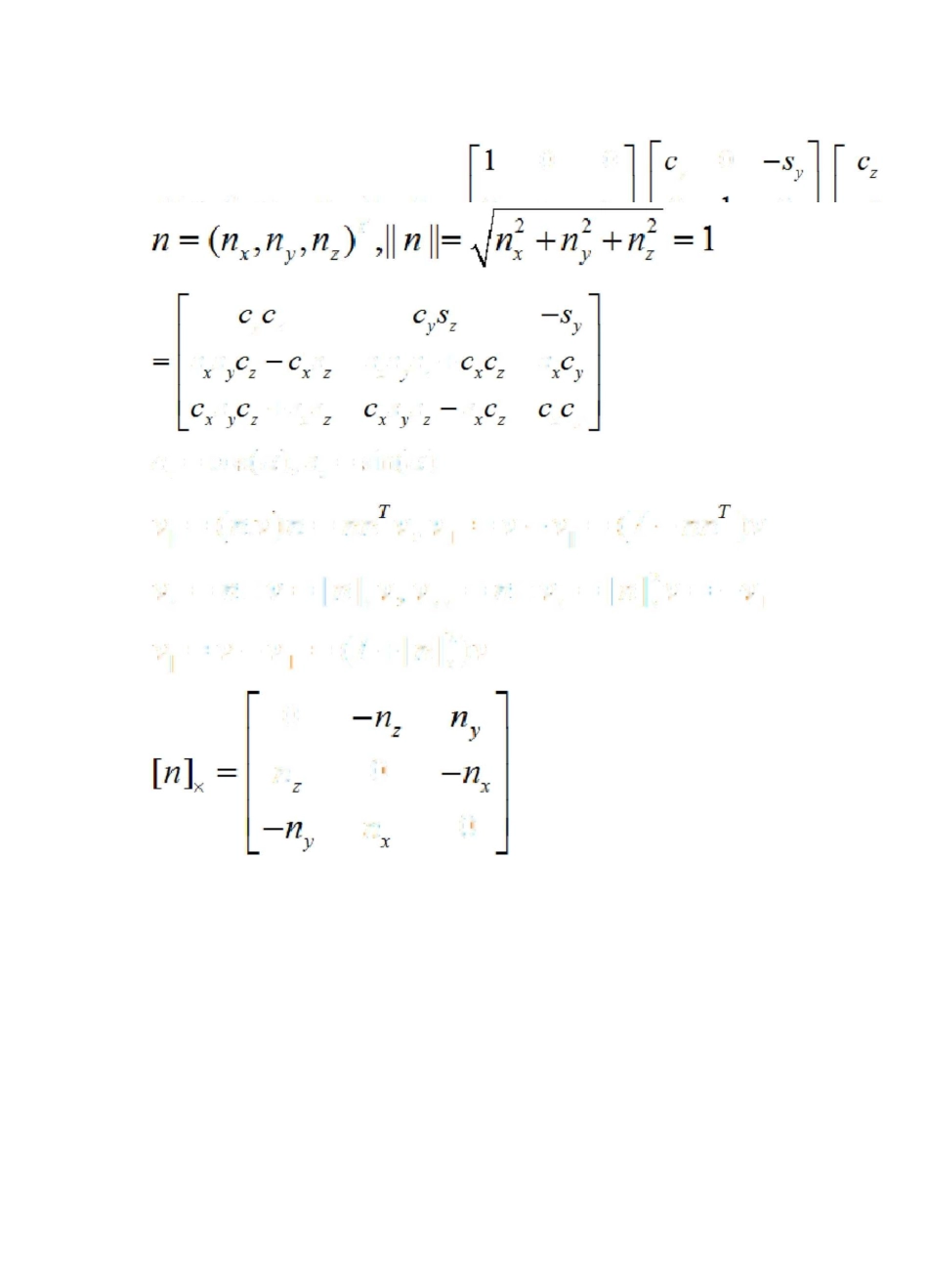三维旋转矩阵的计算VIP免费

三维旋转矩阵的计算旋转矩阵(Rotationmatrix)是在乘以一个向量的时候有改变向量的方向但不改变大小的效果的矩阵。旋转矩阵不包括反演，它可以把右手坐标系改变成左手坐标系或反之。所有旋转加上反演形成了正交矩阵的集合。在三维空间中，旋转变换是最基本的变换类型之一，有多种描述方式，如Euler角、旋转矩阵、旋转轴/旋转角度、四元数等。本文将介绍各种描述方式以及它们之间的转换。1.旋转矩阵用一个3阶正交矩阵来表示旋转变换，是一种最常用的表示方法。容易证明，3阶正交阵的自由度为3。注意，它的行列式必须等于1，当等于-1的时候相当于还做了一个镜像变换。2.Euler角根据Euler定理，在三维空间中，任意一种旋转变换都可以归结为若干个沿着坐标轴旋转的组合，组合的个数不超过三个并且两个相邻的旋转必须沿着不同的坐标轴。因此，可以用三个沿着坐标轴旋转的角度来表示一个变换，称为Euler角。旋转变换是不可交换的，根据旋转顺序的不同，有12种表示方式，分别为：XYZ、XZY、XYX、XZX、YXZ、YZX、YXY、YZY、ZXY、ZYX、ZXZ、ZYZ,可以自由选择其中的一种。对于同一个变换，旋转顺序不同，Euler角也不同，在指定Euler角时应当首先约定旋转顺序。2.1Euler角转化为旋转矩阵不妨设先绕Z轴旋转Y，再绕丫轴旋转B，最后绕X轴旋转a，即旋转顺序为XYZ,旋转矩阵00n0nV|i=(rty)n=nnv,v±=v-vN=(I一nn)v\=WXV=[w]xV.Vxx=nxvx=[w]Jv=-v±旳=v-v±=(I+[n]^vT3.旋转轴/旋转角度用旋转轴的方向向量n和旋转角度e来表示一个旋转，其e>0表示逆时针旋转。3.1旋转轴/旋转角度转化为旋转矩阵设v是任意一个向量，定义000y000c000Xyssss%ssss十wxyyz耳叭①R(g0异)=RjR』R’=cx=cos(or),sx=sin(tz)如下图所示r(9'vvz?]这样，我们建立了一个直角坐标系。设u为v绕轴旋转后得到的向量，则有u±=cos9v±+sinOvy=(sin^[/i]x—cos&[/?]：)—=1it=11丄+%=(I+sin^[w]x+(1—cos^)[w]^)v=R{n,0Rg0)=I+sin0[n\y+(1—cos臼)W]；R即为旋转矩阵。进一步可表示为co=On=(qg尸乞?R(e)=7?(卷&)4.单位四元数(Unitquaternions)四元数由Hamilton于1843年提出，实际上是在四维向量集合上定义了通常的向量加法和新的乘法运算，从而形成了一个环。qY=況]+Jyr+kzi+CD1,q2=ix2+jy2+kz2+(o241+02=Z(X1+尤2)+J®+y2)+疋(Z]+%)+(©+®2)qrq2=(trL+jy\+kzx+®)(迅+jy^+kz2+©)■丄・2丁2--j-Tj-i=j=k=ijk=-\.i=jk=-tga.T■■jT*■■■■j=ki=-ik.k=y=-ji|q||=Jx2^y2+z2+ft?2q称为单位四元数，如果||q||=1。一个单位四元数可以表示三维旋转。用单位四元数表示旋转可以保持一个光滑移动的相机的轨迹，适合动画生成。4.1旋转轴/旋转角度转化为单位四元数根据旋转轴n和旋转角度6，得到单位四元数q4.2单位四元数转化为旋转轴/旋转角度R（q1-2（/+于）2（xy+zco）2（xz-yco）2（xy-za））1-2（兀-+）2（XZ+JZ9）2（yz_Ad?）4.3单位四元数转化为旋转矩阵R（n.^）=7+sin6*[/?]a+（1-cos=Z+2co[vl+2[v]^■0-zZ_22-y一zXZZ0-X,=秽22-x-z一一yX0XZ22-X-y4.4四元数的性质定义四元数的逆、乘法和除法，如下所示弘=（%,刃1）,?2=（叫，®）弘1=（V2，一型）=（一叫，®）q=qxq2=（vtxv2+ft?tv2+fi?2v1?①乌一vi形）q'=qjq?==（片xv2+G^V2一o）^\,-CD^D2一vLR®=R（qJRa）,RS=R（qJR（q；）根据该性质，我们可以对两个旋转变换q1和q2作线性插值，这相当于在四维空间中的超球面上对点q1和q2作球面线性插值。也可以按下面的方法计算Qr=qJq、=（匕®）if<0thenqr=-qr0r=2tan-1（||vr||!a）r）nrIIe（t）=ter?ZG[O?I]%•（『）=（sin£nF,cos|）