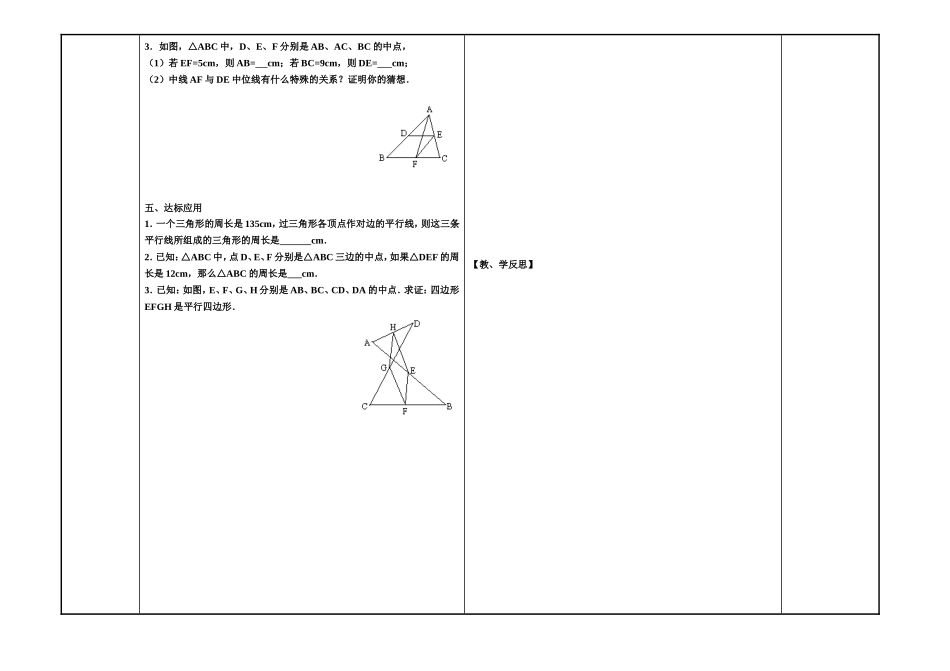
范县城关镇中学导学案年级:八年级学科:数学主备人:王丽娟审核人:初二数学组授课人:班级:小组:姓名:编号:课题《19.1.2平行四边形的判定——三角形的中位线(三)》课型:自学展示课时:1【教师复备或学生纠错栏】例1分析:所证明的结论既有平行关系,又有数量关系,联想已学过的知识,可以把要证明的内容转化到一个平行四边形中,利用平行四边形的对边平行且相等的性质来证明结论成立,从而使问题得到解决,这就需要添加适当的辅助线来构造平行四边形.一、【学习目标】理解三角形中位线的概念,熟练地应用三角形中位线性质进行有关的证明和计算.【学习过程】二、自主学习不动笔墨不读书,拿出你的笔和激情,开始行动吧!【探究】:请同学们思考:将任意一个三角形分成四个全等的三角形,你是如何切割的?图中有几个平行四边形?你是如何判断的?三、合作探究例1如图,点D、E、分别为△ABC边AB、AC的中点,求证:DE∥BC且DE=BC.方法1:方法2:定义:连接三角形两边中点的线段叫做三角形的中位线.(1)想一想:①一个三角形的中位线共有几条?②三角形的中位线与中线有什么区别?(2)三角形的中位线与第三边有怎样的关系?三角形中位线的性质:〖拓展〗:利用这一定理,你能证明出探究中分割出来的四个小三角形全等吗?(口述)例2(补充)已知:如图(1),在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形.四、反馈提升1.如图,A、B两点被池塘隔开,在AB外选一点C,连结AC和BC,并分别找出AC和BC的中点M、N,如果测得MN=20m,那么A、B两点的距离是m,理由是.2.已知:三角形的各边分别为8cm、10cm和12cm,求连结各边中点所成三角形的周长.例2分析:因为已知点E、F、G、H分别是线段的中点,可以设法应用三角形中位线性质找到四边形EFGH的边之间的关系.由于四边形的对角线可以把四边形分成两个三角形,所以添加辅助线,连接AC或BD,构造“三角形中位线”的基本图形后,此题便可得证.3.如图,△ABC中,D、E、F分别是AB、AC、BC的中点,(1)若EF=5cm,则AB=cm;若BC=9cm,则DE=cm;(2)中线AF与DE中位线有什么特殊的关系?证明你的猜想.五、达标应用1.一个三角形的周长是135cm,过三角形各顶点作对边的平行线,则这三条平行线所组成的三角形的周长是cm.2.已知:△ABC中,点D、E、F分别是△ABC三边的中点,如果△DEF的周长是12cm,那么△ABC的周长是cm.3.已知:如图,E、F、G、H分别是AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形.【教、学反思】