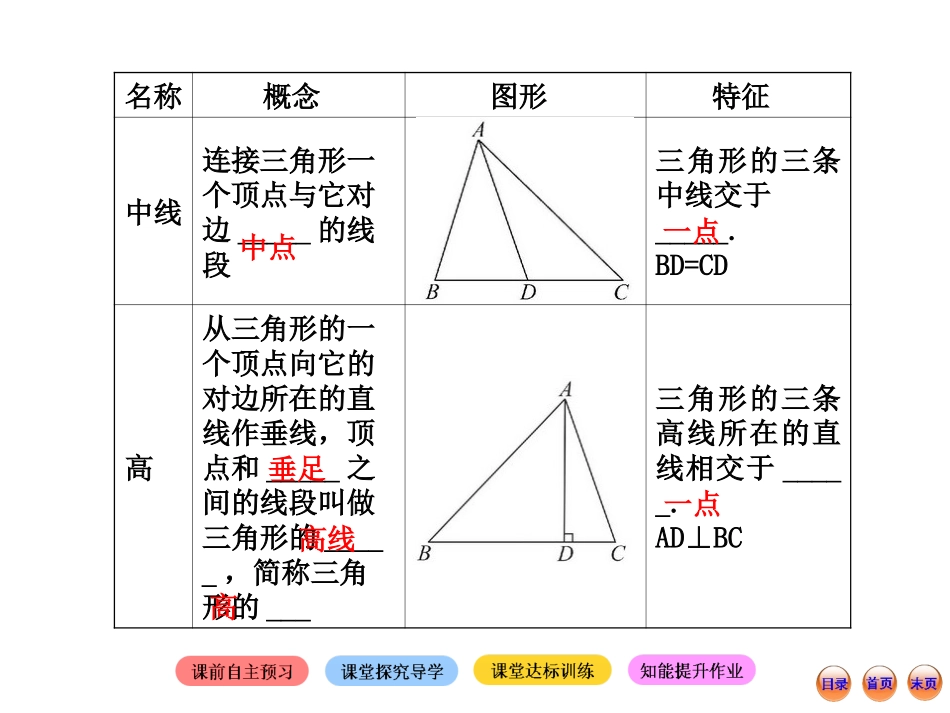
点击进入相应模块第3课时三角形的三种重要线段的概念及特征名称概念图形特征角平分线在三角形中,一个内角的角平分线与它的对边相交,该角顶点与交点之间的_____三角形的三条角平分线交于_____.∠1=∠2线段一点名称概念图形特征中线连接三角形一个顶点与它对边_____的线段三角形的三条中线交于_____.BD=CD高从三角形的一个顶点向它的对边所在的直线作垂线,顶点和_____之间的线段叫做三角形的_____,简称三角形的___三角形的三条高线所在的直线相交于_____.AD⊥BC中点一点垂足高线高一点探究:三角形的三条高的关系:如图,画出锐角三角形、直角三角形和钝角三角形的三条高.①锐角三角形的三条高相交于三角形___部的___个点.②直角三角形的三条高相交于三角形的_________.③钝角三角形的三条高所在直线相交于三角形___部的___个点.【归纳】三角形的三条高所在的直线相交于一点.【点拨】三角形的角平分线、高、中线都是线段.内一直角顶点外一【预习思考】三角形的角平分线和角的平分线是一回事吗?提示:不是.它们均平分一个角,但三角形的角平分线是一条线段,而角的平分线是一条射线.三角形的三种重要线段区分【例1】(9分)如图,在△ABC中,∠BCA是钝角,完成下列画图,并用适当的符号在图中表示:(1)∠ABC的角平分线;(2)AC边上的中线;(3)AC边上的高.【规范解答】如图所示:(1)BE为∠ABC的角平分线,可表示为∠ABE=∠CBE=∠ABC,或∠ABC=2∠ABE=2∠CBE.…………………………………3分特别提醒:△ABC的AC边上的高在三角形外,不要画在三角形内,注意在垂足处标上垂直符号.12(2)BD为AC边上的中线,可表示为AD=CD=AC.……………6分(3)BF为AC边上的高,可表示为BF⊥AC于点F,或∠AFB=90°.……………………………………………………………………9分12【规律总结】三角形的三种重要线段识别的两点注意(1)不要混淆:准确把握三角形三种重要线段的概念,弄清三者的区分.(2)注意数量关系的推理判断:三角形的角平分线可得到两个相等角,三角形的中线可得到两条相等的线段和两个面积相等的三角形,三角形的高可得到垂直关系或直角.【跟踪训练】1.如图所示,在△ABC中,D,E,F是BC边上的三点,且∠1=∠2=∠3=∠4,AE是哪个三角形的角平分线()(A)△ABE(B)△ADF(C)△ABC(D)△ABC,△ADF【解析】选D.因为∠2=∠3,所以AE是△ADF的角平分线.因为∠1=∠2=∠3=∠4,所以∠1+∠2=∠3+∠4,即∠BAE=∠CAE,所以AE是△ABC的角平分线.2.如图,AC⊥BC,CD⊥AB,DE⊥BC,垂足分别为C,D,E,则下列说法不正确的是()(A)AC是△ABC的高(B)DE是△BCD的高(C)DE是△ABE的高(D)AD是△ACD的高【解析】选C.选项A的说法符合高的概念,故正确;选项B的说法符合高的概念,故正确;选项C,DE是△BDC,△BDE,△EDC的高,不是△ABE的高,故错误;选项D的说法符合高的概念,故正确.3.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是()(A)锐角三角形(B)钝角三角形(C)直角三角形(D)都有可能【解析】选C.一个三角形的三条高的交点恰是三角形的一个顶点,则这个三角形是直角三角形.三角形中三条重要线段的综合应用【例2】(7分)已知在△ABC中,∠C>∠B,AD是BC边上的高,AE平分∠BAC,试说明∠DAE=(∠C-∠B).【规范解答】因为AD⊥BC,所以∠BDA=90°,所以∠BAD=90°-∠B.………………………………………2分12又因为AE平分∠BAC,所以∠BAE=∠BAC=(180°-∠B-∠C),………………………………………4分所以∠DAE=∠BAD-∠BAE=90°-∠B-(180°-∠B-∠C)=90°-∠B-90°+∠B+∠C=∠C-∠B=(∠C-∠B).………………………………7分特别提醒:不要直接在△ADE中求∠DAE.1212121212121212【规律总结】三角形的角平分线和高的综合应用的一般思路先确定欲求角在哪个三角形中,然后由角平分线或高确定角的数量关系,最后由三角形的内角和求出相关角的关系或度数.【跟踪训练】4.如图,AD,BE都是△ABC的高,则与∠CBE一定相等的角是()(A)∠ABE(B)∠BAD(C)∠DAC(D)∠C【解析】选C.在△BEC和△ADC中,∠C是公共角,∠ADC=∠BEC=90°,所以∠CBE=∠DAC.5.如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°...