几何类应用问题VIP免费

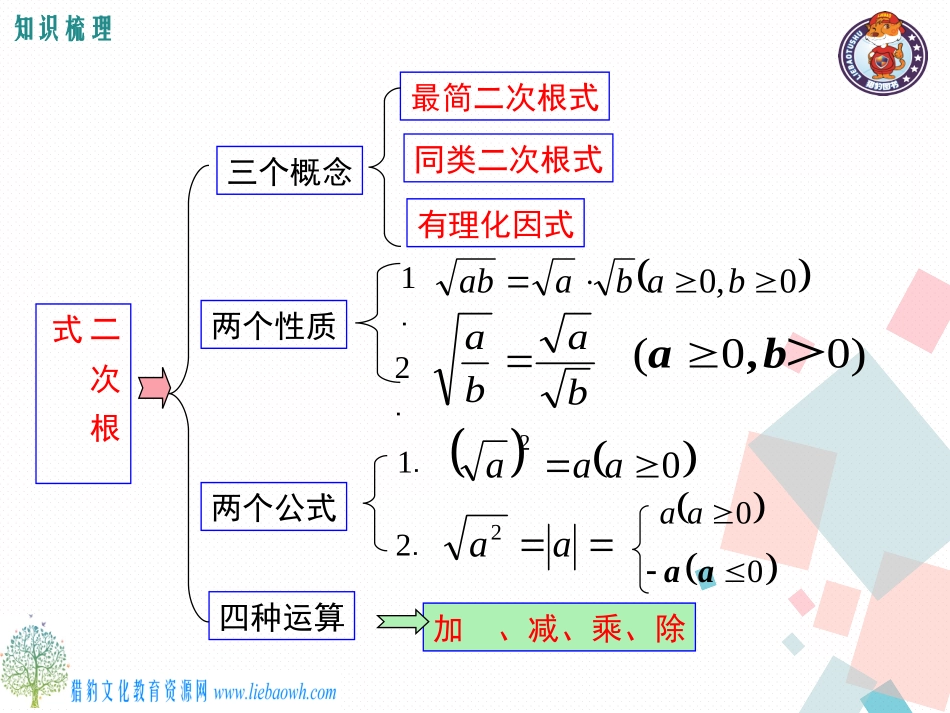
复习和小结第21章二次根式导入新课讲授新课当堂练习课堂小结加、减、乘、除二次根式三个概念两个性质两个公式四种运算最简二次根式同类二次根式有理化因式baba(00)a,b＞0,0babaab1.2.2.1.02aaaaa20aa0aa知识梳理1．二次根式的概念一般地，形如____(a≥0)的式子叫做二次根式；对于二次根式的理解：①带有根号；②被开方数是非负数,即a≥0.[易错点]二次根式中，被开方数一定是非负数，否则就没有意义.2．二次根式的性质3．最简二次根式满足下列两个条件的二次根式，叫做最简二次根式．(1)被开方数不含_______；(2)被开方数中不含能___________的因数或因式．开得尽方分母220;0000aaaaaaaa,aa.＞，＜4．二次根式的运算＝______(a≥0，b≥0)；＝____(a≥0，b>0)．二次根式加减时，可以先将二次根式化成_____________，再将________________的二次根式进行合并．被开方数相同最简二次根式abab1.当x_____时，有意义.x33.求下列二次根式中字母的取值范围.153xx解得-5≤x＜3解：5030x,x＞，①②说明：二次根式被开方数不小于0，所以求二次根式中字母的取值范围常转化为不等式（组）.≤3a=4考点分类确定二次根式中被开方数所含字母的取值范围一2.有意义的条件是.44aa1.已知：+=0,求x-y的值.yx24x2.已知x,y为实数,且+3(y-2)2=0,则x-y的值为()A.3B.-3C.1D.-11x解：由题意，得x-4=0且2x+y=0解得x=4,y=-8x-y=4-(-8)=4+8=12D二次根式的非负性的应用二方法技巧初中阶段主要涉及三种非负数：≥0，≥0，a2≥0.如果若干个非负数的和为0，那么这若干个非负数都必为0.即由a≥0，b≥0，c≥0且a＋b＋c＝0，一定得到a＝b＝c＝0，这是求一个方程中含有多个未知数的有效方法之一.aa二次根式性质的应用三设＝a，＝b，用含a，b的式子表示，则下列表示正确的是()A．0.03abB．3abC．0.1ab3D．0.1a3b23054.C二次根式的化简四A二次根式的运算五1.确定二次根式中被开方数所含字母的取值范围2.二次根式的非负性的应用3.二次根式性质的应用4.二次根式的化简5.二次根式的运算复习归纳C0课后演练33．若１＜．若１＜xx＜４，则化简＜４，则化简的结果是＿＿＿＿＿的结果是＿＿＿＿＿22(4)(1)xx4.下列各式中，是最简二次根式的是（）3BA8.B70.C99.1D.x55..下列各式中哪些是二次根式？那些不是？为什么？下列各式中哪些是二次根式？那些不是？为什么？153a100x3522ab21a144221aa⑧⑧⑦⑦⑥⑥⑤⑤④④①①②②③③a<0-(a2+1)<0(a-1)2≥06.计算：（1）312-248+8（2）445×35÷（-3410）（3）80-（315+4545）=-23+22=-8515=45511221若a为底,b为腰,此时底边上的高为2142721422222∴三角形的面积为(2)若满足上式的a,b为等腰三角形的两边,求这个等腰三角形的面积.设a、b为实数,且|2-a|+b-2=0√22ab，解:若a为腰,b为底,此时底边上的高为11472222∴三角形的面积为2211（）ab（1）求、的值.7.（2）如图所示，AD⊥DC于D，BC⊥CD于C，ABPDC若点P为线段CD上动点.，10已知△ABP的一边AB=①则AD=____BC=____12（1）在如图所示的4×4的方格中画出格点△ABP，使三角形的三边为，10，5，58.②设DP=a,请用含a的代数式表示AP，BP,则AP=_________，BP=__________.24a2(3)1a③当a=1时，则PA+PB=______,25当a=3,则PA+PB=______.④PA+PB是否存在一个最小值？113