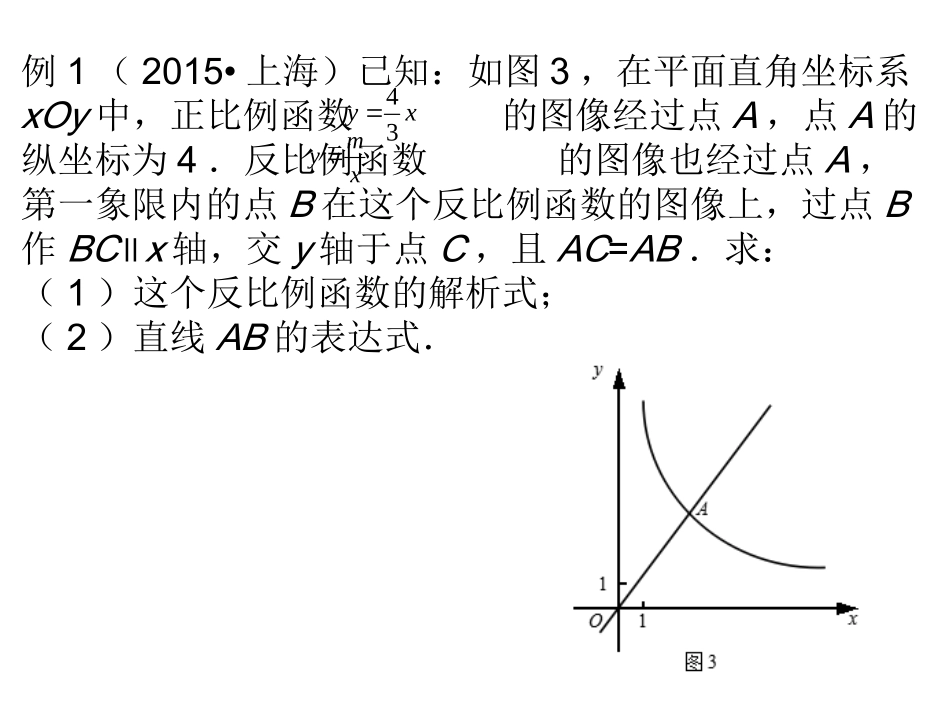
专题复习——函数应用知识点梳理:1.基本概念:一次函数(正比例函数)、反比例函数2.基本方法、思想:待定系数法求函数解析式、方程思想3.涉及应用问题:交点、面积问题;物理问题;行程问题;方案设计问题例1(2015•上海)已知:如图3,在平面直角坐标系xOy中,正比例函数的图像经过点A,点A的纵坐标为4.反比例函数的图像也经过点A,第一象限内的点B在这个反比例函数的图像上,过点B作BC∥x轴,交y轴于点C,且AC=AB.求:(1)这个反比例函数的解析式;(2)直线AB的表达式.xy34xmy1.(2013•上海)已知平面直角坐标系xOy(如图),直线经过第一、二、三象限,与y轴交于点B,点A(2,t)在这条直线上,联结AO,△AOB的面积等于1.(1)求b的值;(2)如果反比例函数(k是常量,k≠0)的图象经过点A,求这个反比例函数的解析式.练习:例2(2014•上海)已知水银体温计的读数y(℃)与水银柱的长度x(cm)之间是一次函数关系.现有一支水银体温计,其部分刻度线不清晰(如图),表中记录的是该体温计部分清晰刻度线及其对应水银柱的长度.(1)求y关于x的函数关系式(不需要写出函数的定义域)(2)用该体温计测体温时,水银柱的长度为6.2cm,求此时体温计的读数.水银柱的长度x(cm)4.2…8.2[来源:学科网ZXXK]9.8体温计的读数y(℃)35.0…40.042.0练习:3.(2014•黄浦二模)已知弹簧在其弹性限度内,它的长度y(厘米)与所挂重物质量x(千克)的关系可表示为的形式,其中称为弹力系数,测得弹簧A的长度与所挂重物(不超过弹性限度)的关系如图7-1所示.(1)求弹簧A的弹力系数;(2)假设在其它条件不变的情况下,弹簧的弹力系数与弹簧的直径(如图7-2所示)成正比例.已知弹簧B的直径是弹簧A的1.5倍,且其它条件均与弹簧A相同(包括不挂重物时的长度).当弹簧B挂一重物后,测得此时弹簧长度为9厘米,求该重物的质量.y(厘米)x(千克)81048Odykxbkkd例3(2015•长宁二模)在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回甲地.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的关系如图所示.根据图像回答下列问题:(1)汽车在乙地卸货停留(h);(2)求汽车返回甲城时y与x的函数解析式,并写出定义域(3)求这辆汽车从甲地出发4h时与甲地的距离.练习:4.(2016•闸北二模)甲骑自行车从A地出发前往B地,同时乙步行从B地出发前往A地,如图所示,、分别表示甲、乙离开A地y(km)与已用时间x(h)之间的关系,且直线与直线相交于点M.(1)求与x的函数关系式(不必注明自变量x的取值范围);(2)求A、B两地之间距离.y甲y乙y甲y乙y甲x(h)My乙y甲y(km)O27.50.5练习:5.(2014•浦东二模)甲、乙两车都从A地前往B地,如图分别表示甲、乙两车离A地的距离S(千米)与时间t(分钟)的函数关系.已知甲车出发10分钟后乙车才出发,甲车中途因故停止行驶一段时间后按原速继续驶向B地,最终甲、乙两车同时到达B地,根据图中提供的信息解答下列问题:(1)甲、乙两车行驶时的速度分别为多少?(2)乙车出发多少分钟后第一次与甲车相遇?(3)甲车中途因故障停止行驶的时间为多少分钟?例4(2015•闸北二模)某公司的物流业务原来由A运输队承接,已知其收费标准y(元)与运输所跑路程x(公里)之间是某种函数关系.其中部分数据如下表所示:x(公里)80120180200…y(元)200300450500…(1)写出y(元)关于x(公里)的函数解析式;(2)由于行业竞争激烈,现B运输队表示:若公司每次支付200元的汽车租赁费,则可按每公里0.9元收费.请写出B运输队每次收费y(元)关于所跑路程x(公里)的函数解析式;(不需写出定义域)(3)如果该公司有一笔路程500公里的运输业务,请通过计算说明应该选择哪家运输队?课堂小结:一次函数、正比例函数、反比例函数;待定系数法:求解两个未知数,要列二元一次方程组;涉及的应用问题:交点、面积问题;物理问题;行程问题;方案设计问题2.(2015•普陀二模)已知:如图7,在平面直角坐标系xOy中,直线与x轴交于点A,在第一象限内与反比例函数图像交于点B,BC垂直于x轴,垂足为点C,且OC=2AO.求(1)点的坐标;(2)反...