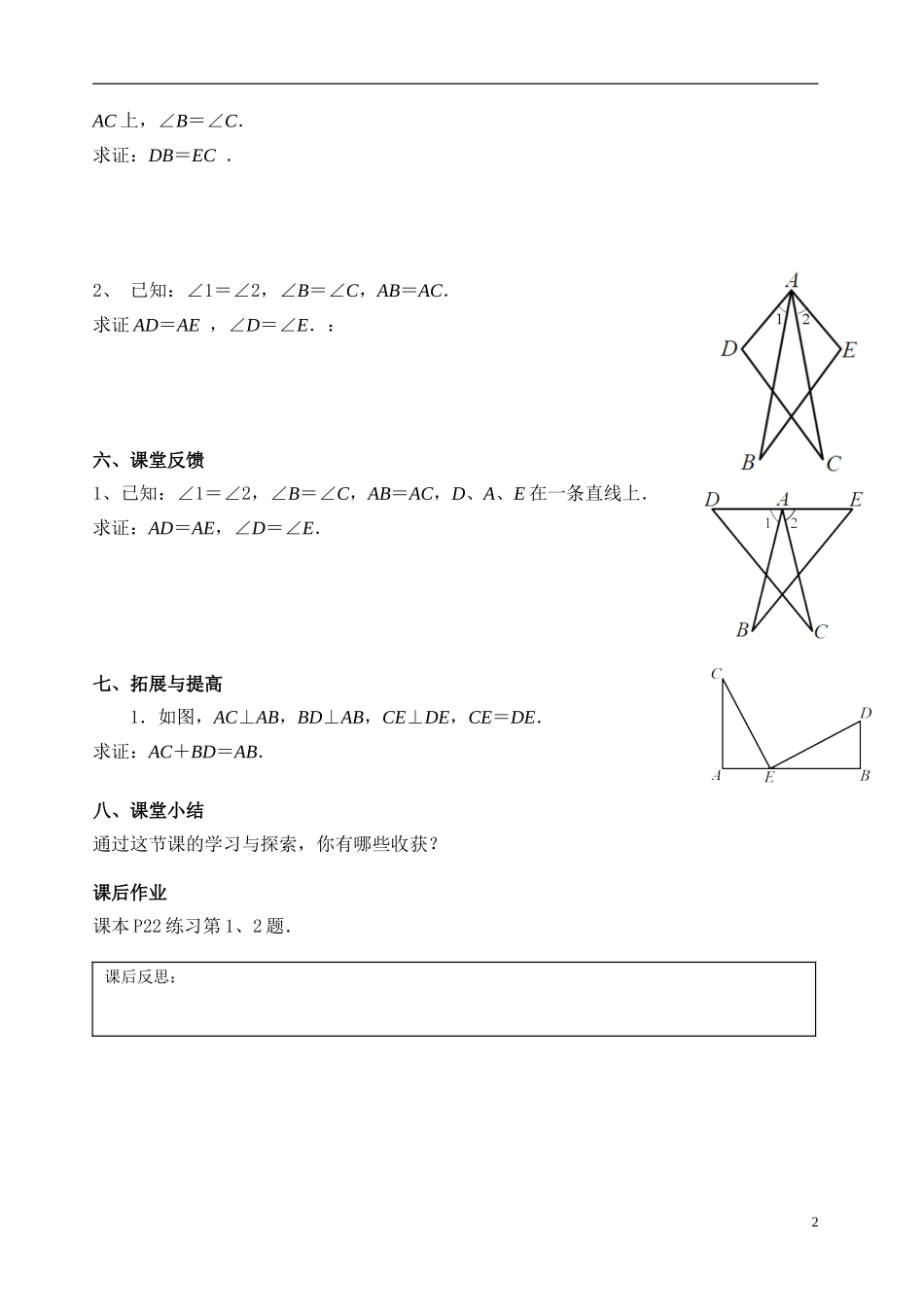
镇江市第十中学生本课堂八年级数学教案1.3探索三角形全等的条件(6)主备:仲建新审核:执教:使用时间:教学目标1.会应用“角边角”“角角边”定理证明两个三角形全等,进而证明线段或角相等;2.进一步渗透综合、分析等思想方法,从而提高学生演绎推理的条理性和逻辑性.学习重难点:灵活应用“角边角”“角角边”定理证明两个三角形全等,进而证明线段或角相等.教学过程:一、回顾与思考:三角形全等判定方法方法1:方法2:方法3:如图,已知AD平分∠BAC,要使△ABD≌△ACD,(1)根据“SAS”需添加条件________;(2)根据“ASA”需添加条件________;(3)根据“AAS”需添加条件________.二、分析与讨论1.如图,∠A=∠B,∠1=∠2,EA=EB,你能证明AC=BD吗?2.如图,点C、F在AD上,且AF=DC,∠B=∠E,∠A=∠D,你能证明AB=DE吗?三、归纳与总结1.为了利用“ASA”或“AAS”定理判定两个三角形全等,有时需要先把已知中的某个条件,转变为判定三角形全等的直接条件.2.证明两条线段相等或两个角相等可以通过证明它们所在的两个三角形全等而得到.四、理解与应用例已知:如图,点A、B、C、D在一条直线上,EA∥FB,EC∥FD,EA=FB.求证:AB=CD.五、巩固与练习1、已知:如图,AB=AC,点D、E分别在AB、1AC上,∠B=∠C.求证:DB=EC.2、已知:∠1=∠2,∠B=∠C,AB=AC.求证AD=AE,∠D=∠E.:六、课堂反馈1、已知:∠1=∠2,∠B=∠C,AB=AC,D、A、E在一条直线上.求证:AD=AE,∠D=∠E.七、拓展与提高1.如图,AC⊥AB,BD⊥AB,CE⊥DE,CE=DE.求证:AC+BD=AB.八、课堂小结通过这节课的学习与探索,你有哪些收获?课后作业课本P22练习第1、2题.2课后反思: