探究与发现子集的个数有多少VIP免费

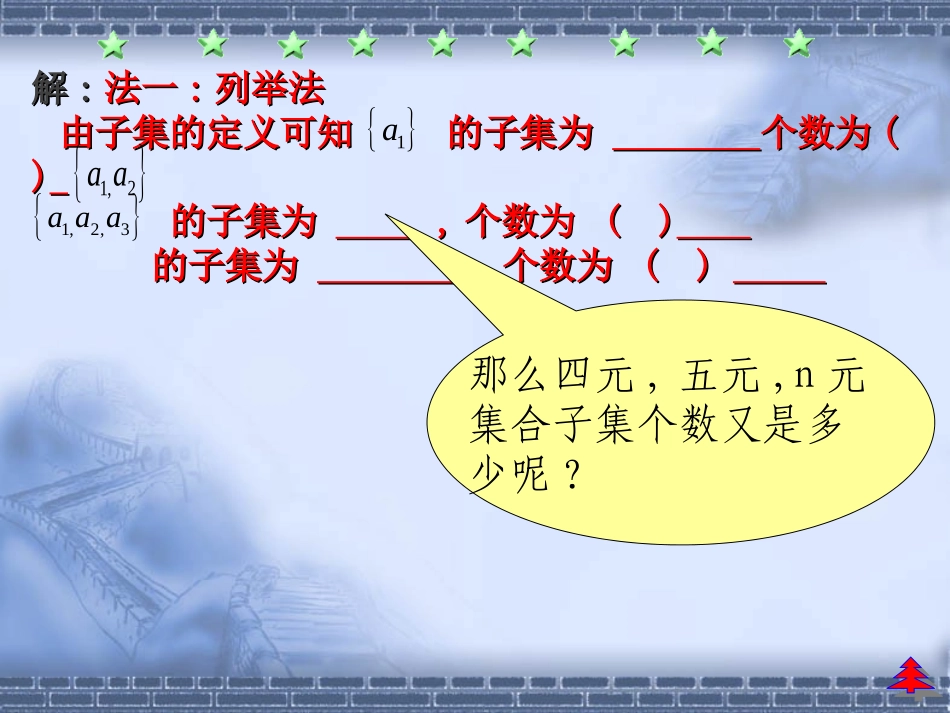
探究与发现子集的个数有多少?1.提出问题：回顾子集的概念2.集合,,子集及其个数分别是多少?的情况又如何呢?那么,这些结论是如何得到的呢?1a1,2aa1,2,3aaa1,2,3......naaaa解解::法一法一::列举法列举法由子集的定义可知的子集为由子集的定义可知的子集为个数为个数为(())的子集为的子集为,,个数为个数为()()的子集为的子集为个数为个数为()()那么四元,五元,n元集合子集个数又是多少呢?1a1,2aa1,2,3aaa法二:树状图以为例1,2,3aaa法三:分步计数原理显然元素(i=1,2,3)与各子集的关系只有两种:属于子集或不属于子集.这样,我们可以考虑集合中的每一个元素属不属于某个子集的方法来得到一个子集.则确定子集的个数可以分为三个步骤.根据分布乘法计数原理2×2×2=3232一般的我们有n元集合的不同子集有个.2nia法四:二进制法(以为例)对于一个集合的子集,属于或不属于子集二者必居其一,且只居其一.我们用1表示是,用0表示否,那么二进制数100就表示子集.表格表示如下:元素元素元素对应的子集0000010101000111011101111,2,3aaa此过程是按照数字顺序列举8个三位的二进制数,从0的二进制数000到表示7的二进制数111,通过有序的列举,得到了8种不同的排法,且做到不重不漏.更重要的是发现了一般规律:n元集合A的子集对应一个n位的二进制数,第i个位置上是0,表示集合A的第i个元素不再相应的子集中,第i个位置上是1表示集合A的第i个元素在相应的子集中,这样根据分步计数原理可以得到n位的二进制数000......0(表示0)到111...1(表示-1)共有个,于是n元集合的子集共有个2n2n2n高考链接:1【2014高考湖北理】设为全集，A,B是集合，则“存在集合C使得是“”的（）A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件2.【2015高考湖南理】.设A，B是两个集合，则“”是“”的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.【2016高考天津理】已知集合则=（）（A）（B）（C）（D）UCCBCAU,BA{1,2,3,4},{|32},AByyxxA，AB{1}{4}{1,3}{1,4}通过四种方法的研究,我们得到:n元集合子集的个数的结论及其运算原理,并且明白从具体事例的分析中得到规律性的猜想,再通过严格的数学推理获得一般结论是研究问题的基本方法.OM