14.2.2全等三角形的判定(ASA)VIP免费

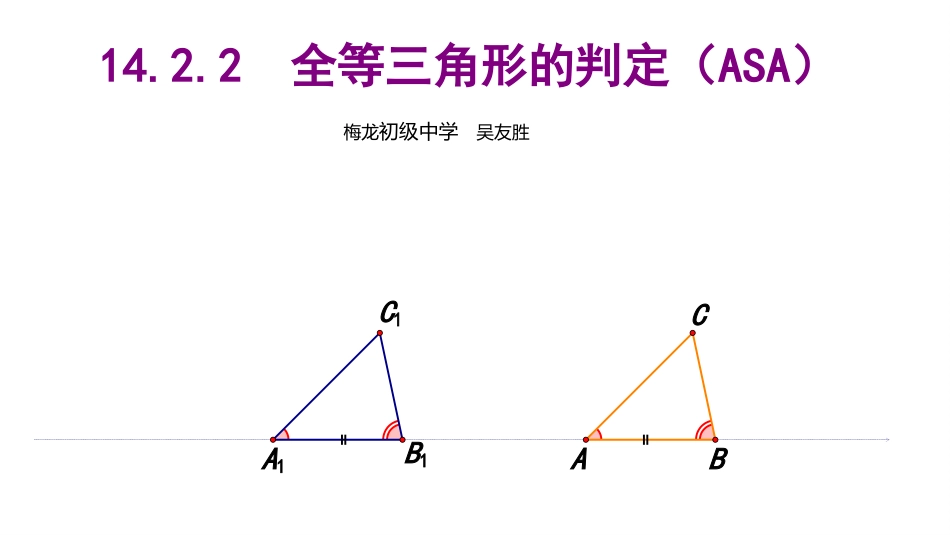
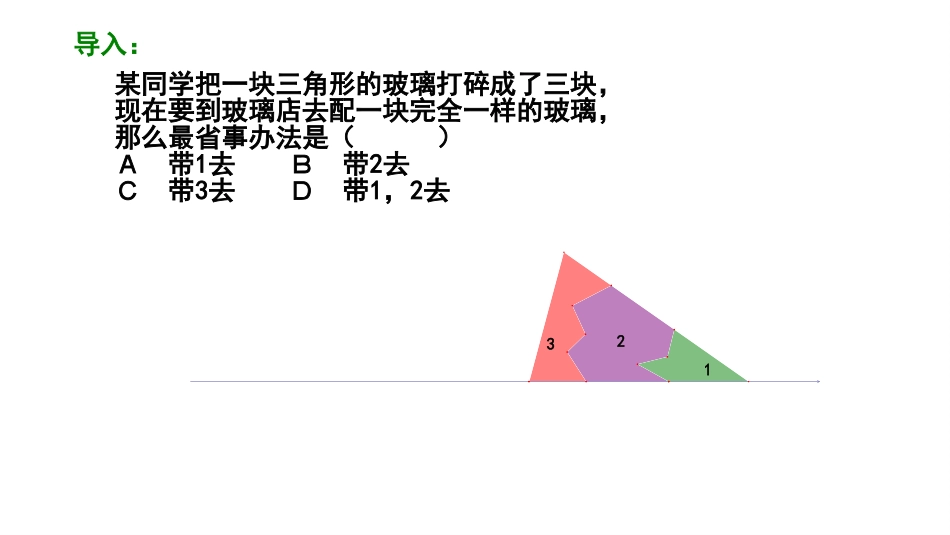
14.2.2全等三角形的判定（ASA）B1C1CBAA1梅龙初级中学吴友胜导入：某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事办法是（）Ａ带1去Ｂ带2去Ｃ带3去Ｄ带1，2去123操作题已知：ABC求作：DEF,使∠E=∠B,EF=BC,∠F=∠C.ACB判定两个三角形全等方法2（基本事实）两角及其夹边分别相等的两个三角形全等简记为“角边角”或“ＡＳＡ”EFCBAD在ABC与DEF中∠A＝∠D已知()AB＝DE已知()∠B＝∠E已知()∴ABCDEFASA()几何符号语言思考1：如图AC与BD相交于O点，则1、图中可看出相等的是＝2、要证ABOCDO还需要个条件，3、请补充条件，填写证明方案。21ACBOD2431CDBA证明：已知∠DBA＝180°-∠3∠CBA＝180°-∠4而∠3＝∠4∴∠DBA＝∠CBA在ABD与ABC中∠1＝∠2已知()AB＝AB公共边()∠DBA＝∠CBA已知()∴ABDABCASA()∴DB=CB全等三角形对应边相等()例1已知：如图∠1=∠2,∠3=∠4求证：DB＝CB例2已知：如图∠1＝∠2，∠ABC＝∠DFE，BE＝FC求证：ABCDFE12DFACBE证明：由BE＝FC∴BE+EC＝FC+EC即BC＝FE在ABC与DFE中∠ABC＝∠DFEBC＝FE∠2＝∠1∴ABCDFEASA()随堂练习1已知：如图∠1＝∠2，∠ABC＝∠DCB求证：ABCDCB12DCACBB12DCACBB12DCACBB随堂练习2：如图ACB，DEF为Ｒt,∠C,∠E为Ｒt∠，且CB＝EF，AB⊥DE求证：ABCDFEFEABCD归纳总结：判定2（基本事实）两角及其夹边分别相等的两个三角形全等简记为“角边角”或“ＡＳＡ”FCEBDA在ABC与DEF中∠A＝∠D已知()AB＝DE已知()∠B＝∠E已知()∴ABCDEFASA()