3.2基本不等式与最大(小)值VIP免费

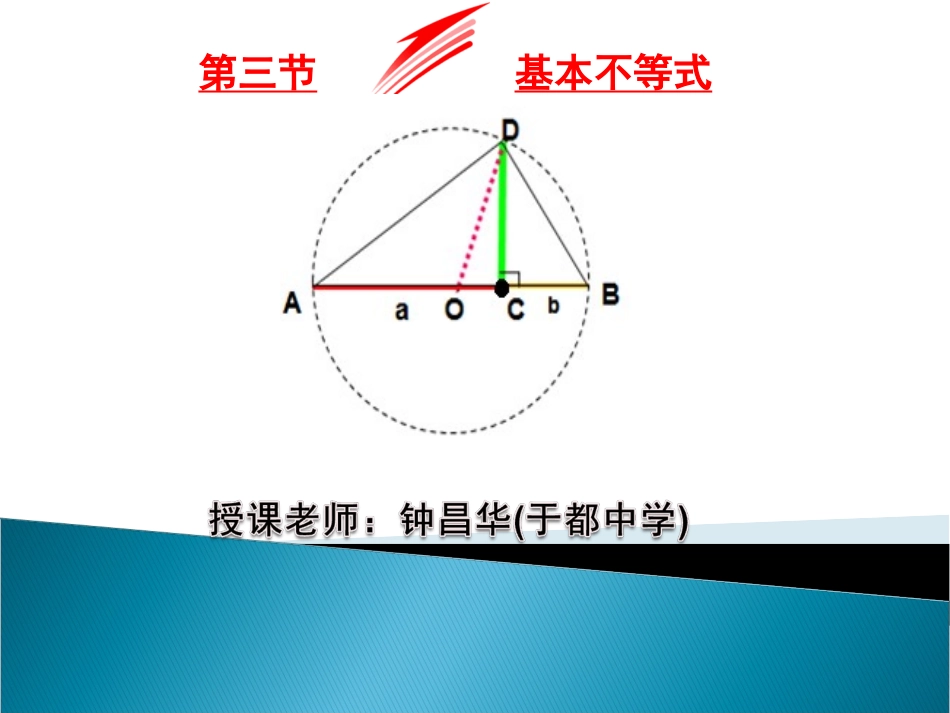
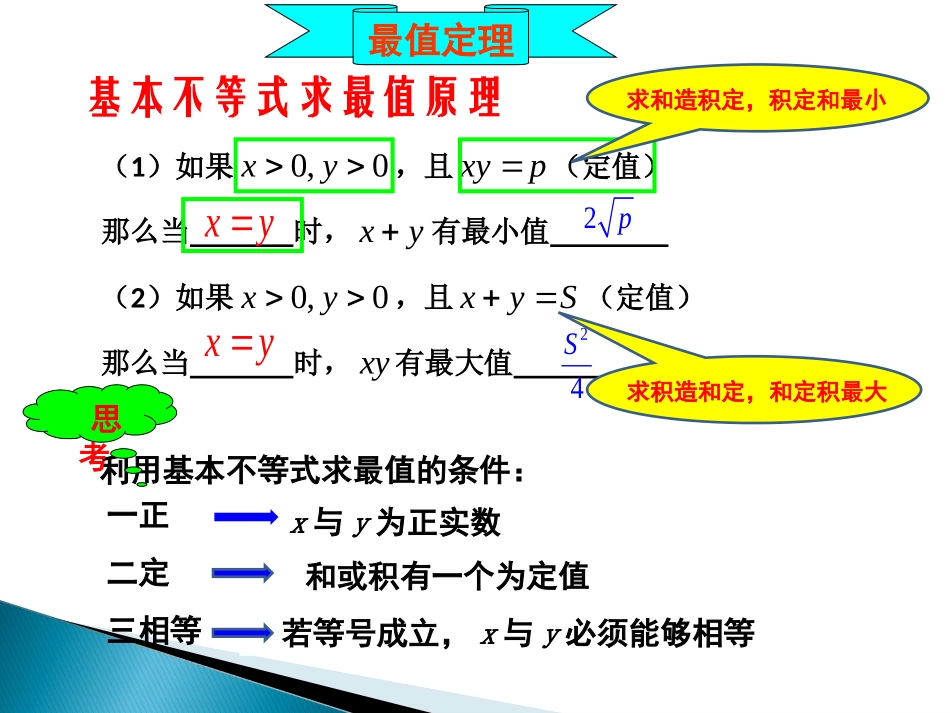
第三节基本不等式,.2ababRab若，则定理222,,2.abRabab如果那么定理1()ab时，且仅当等号成立当()ab时，且仅当等号成立当22224(1)2ababababab（），，当且仅基本不当时，等等式的常见变号成立式；算术平均数几何平均数（1）如果0,0xy，且xyp（定值）那么当时，xy有最小值（2）如果0,0xy，且xyS（定值）那么当时，xy有最大值基本不等式求最值原理xy2p最值定理xy24S利用基本不等式求最值的条件：一正二定三相等x与y为正实数和或积有一个为定值思考若等号成立，x与y必须能够相等求和造积定，积定和最小求积造和定，和定积最大0,0,3;xyxyxy思考题：已知求2的最小值求和造积定，积定和最小0,0,32+2226,2266=6,6262xyxyxyxyxyxyxyxy解，当且仅当2时，取“”当时，2的值最小，最小值为一正二定三相等1.求和的最小值造积为定值，积定和最小2.求积的最大值造和为定值，和定积最大均值不等式的使用方向：方法1:直接法41()2(1)2,();(2)2,();(3)6,();fxxxxfxxfxxfx【例】已知若求的最小值若求的最大值若求的最小值(1)2,2044()(2)2242622xxfxxxxx解：4(2)==42xxx当且仅当时，即时取等号4()6xfx时，取得最小值凑定值42()2(1)2,();(2)2,();(3)6,();fxxxxfxxfxxfx【例】已知若求的最小值若求的最大值若求的最小值(2)22044()(2)2-242-222-xxfxxxxx解：4(2)==02xxx当且仅当时，即时取等号0()-2xfx时，取得最大值创造条件42()2(1)2,();(2)2,();(3)6,();fxxxxfxxfxxfx【例】已知若求的最小值若求的最大值若求的最小值44(3)()(2)222fxxxxx解：42(4),()2xttgttt令则4()2[2,)gtttt在是增函数4()2=4gtttt在时取得最大值7()6fxx在时取得最大值7另找途径2,()(25)5xfxxx：已知0变式2求的最大值4()2(2),()2fxxxfxx变式1：已知求的最小值4()2-2+4(2)2fxxxx变形：（）1()[5(25)]5fxxx变形：凑积为定值凑和为定值1利用基本不等式解决最值问题时，须注意“一正、二定、三相等”．三者．缺一不可123.凑定值，常常可利用以下几种途径：加减常数凑出两项的积为定值；通过乘除系数凑两项的和为定值；通过分式裂项凑出两2项的积为定值；方法2：配凑法题型一配凑法求最值111,xy方法一：把式子整理成用1代换(10)1xyxx方法三：函数思想，,xyxyxyxyxy方法二：注意到式子中有及，把转化为解关于整体的不等式20,0,xyxyxyxy例：已知求的最小值。题型一配凑法求最值例题讲解210,0,24xyxyxy已知求+的最小值。变式1：的最大值。求已知xyxyyxyx,1,0,0变式2：的最大值。则满足若实数yxxyyxyx,1,22变式3：20,,430xyRxxyxy若满足则的最小值。变式4：“1”代换转化xy不等式转化x+y不等式转化x的函数,,2131abababab:给出和为定值,求倒数和的最"小值?如:已知12求"代换的最小值方法3:常数代换:给出式子中既有和的形式也有积的形式,利用均值不等式转化只有"和"或"积"不等式,再通过解目目标整体法标不等式方法4:目标整体法,,abab:给出的关系式,求关于式子的最值?只要利用它们之的关系,把所求函数思想(消元法)转化一元函数问题方法5:消元法1．利用均值不等式求最值时，必须同时满足三个条件：________、________、__________.2．连续两次使用不等式变形时要保持前后等号成立________的一致性．一正二定三相等条件特别注意3355.0,0,22ababababab作业：1已知证明：(1)（）(+)4(2)3311.0,0,36?abababababab2已知且(1)证明：求+的最小值(2)是否存在，使得2并说明理由