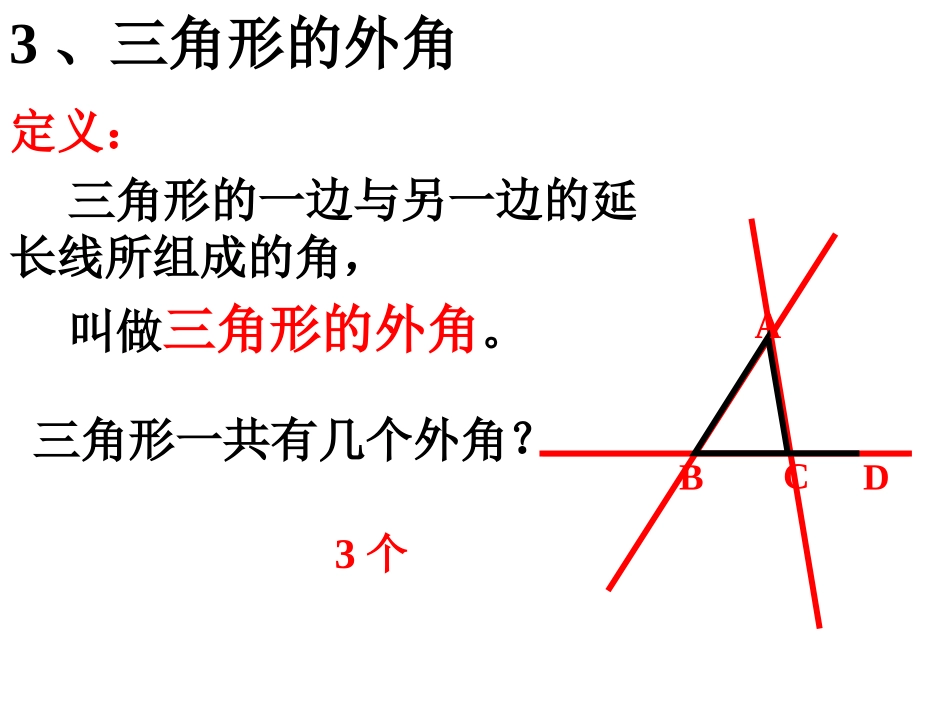
7.5.2关注三角形的外角学习目标:1.掌握三角形内角和定理的两个推论及其证明。2.体会几何中简单不等关系的证明。3.学习从内和外、相等和不等的不同角度对三角形的角作更全面的思考。3、三角形的外角定义:三角形的一边与另一边的延长线所组成的角,叫做三角形的外角。DABC三角形一共有几个外角?3个导学:阅读课本181页例2前部分(3分钟)1.会用符号语言和文字语言描述三角形的外角与内角的关系。2.和同伴交流你们是怎样证明三角形内角和定理的两个推论的。3.什么是推论?推论与公理、定理的关系?证明:∵∠4+2+3=180°∠∠(三角形内角和定理)证明:三角形的一个外角等于和它不相邻的两个内角的和DABC1234已知:如图,∠1是△ABC的一个外角.求证:∠1=2+3∠∠∴∠2+3=∠180°-4∠又∵∠1+4=180°∠∴∠1=180°-4∠∴∠1=2+3(∠∠等量代换)证明:三角形的一个外角大于任何一个和它不相邻的内角已知:如图,∠1是△ABC的一个外角.求证:∠1>2,1>3∠∠∠DABC123证明:∵∠1=2+3∠∠(三角形的一个外角等于和它不相邻的两内角和)∴∠1>2,1>3∠∠∠像这样,由一个公理或定理直接推出的定理,叫做这个公理或定理的推论推论可以当作定理使用.三角形的一个外角大于任何一个和它不相邻的内角.关注▲外角☞☞ABCD123三角形内角和定理的推论三角形的一个外角等于和它不相邻的两个内角的和.推论1:推论2:△ABC中,∠1=2+3∠∠△ABC中,∠1>∠2,∠1>∠3这个结论以后可以直接运用.1、已知:如图,在△ABC中,外角∠DCA=100°,∠A=45°。求:∠B和∠ACB的大小.ABCD解:DCA∵∠是△ABC的一个外角(已知),∴∠B=DCA—A=100°—45°=55°∠∠又∵∠DCA+BCA=180°(1∠平角=180°).∴∠ACB=80°(等式的性质).100°45°(三角形的一个外角等于和它不相邻的两个内角的和).训练反馈ACBDFE1140048025022、如图,求∠1、∠2的度数训练反馈3、已知:如图,在△ABC中,1∠是它的一个外角,E为边AC上一点,延长BC到D,连接DE.求证:1>2.∠∠证明:1∵∠是△ABC的一个外角(已知),∴∠1>3∠∵∠3是△CDE的一个外角(外角定义).∴∠3>2∠∴∠1>2(∠不等式的性质).CABF1345ED2(三角形的一个外角大于任何一个和它不相邻的内角).(三角形的一个外角大于任何一个和它不相邻的内角).训练反馈探究一:思考课本181页例2,与同伴交流你是怎样想的,你们的方法一样吗?例2已知:如图6-13,在△ABC中,AD平分外角∠EAC,B=C.∠∠求证:ADBC.∥ACDBE分析:要证明AD∥BC,只需要证明“同位角相等”,“内错角相等”或“同旁内角互补”.312例题证明:∵∠1+4=180°∠∠2+5=180°∠∠3+6=180°∠∴∠1+2+3+4+5+6∠∠∠∠∠=3×180°=540°又∵∠4+5+6=180°(∠∠三角形内角和定理)∴∠1+2+3=540°—180°=360°∠∠1、已知:∠1,∠2,∠3是△ABC的三个外角.求证:∠1+∠2+∠3=360°.CAB312645训练反馈2、已知:如图求证:(1)BDC>A;∠∠(2)BDC=A+B+C.∠∠∠∠BCADE知识升华BCAD回味无穷三角形内角和定理三角形三个内角的和等于1800.△ABC中,∠A+∠B+∠C=1800.推论1:三角形的一个外角等于和它不相邻的两个内角的和.推论2:三角形的一个外角大于任何一个和它不相邻的内角.小结拓展小测验1、下列哪几种说法正确?(1)∠B
B∠BEAHCD2、如图,把△ACB沿DE折叠,当点A落在四边形BCED内部时,∠DAE与∠1、∠2之间有一种数量关系保持不变,这一规律是()A.∠A=1+2B∠∠、2A=1+2∠∠∠C、3A=21+2D∠∠∠、3A=2∠(∠1+2∠)BDAACE12B思维拓展:•1、(1)如图(甲),在五角星图形中,求∠A+B+C+D+E∠∠∠∠的度数。(2)把图(乙)、(丙)叫蜕化的五角星,问它们的五角之和与五角星图形的五角之和仍相等吗?为什么?AEABCDAE(甲)EBCDDCB(乙)(丙)YucaiMiddleschoolTengzhouShandong山东滕州育才中学课堂小结通过本节课的学习,你有何收获?