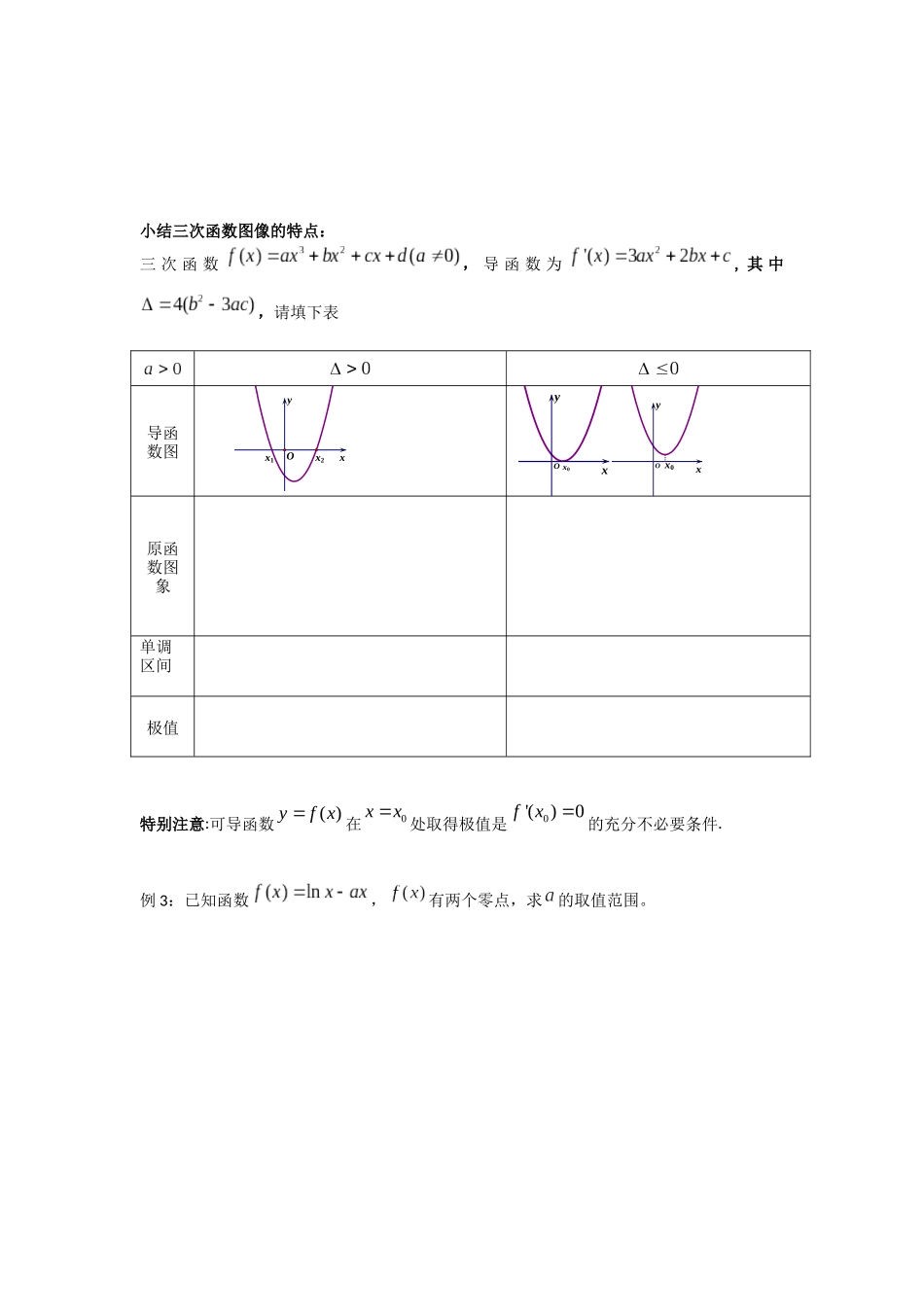
导数在研究函数中的应用(2)【教学目标】1.了解函数极值与最值的概念;会求函数的极值与最值。2.掌握函数有解问题与恒成立问题的常见处理方法。3.在解决问题中体会数形结合与分类讨论思想在解题中的应用。【知识梳理】1.极值的概念一般地,当函数在点处连续时,且,①如果在附近的左侧,右侧,那么是_________;②如果在附近的左侧,右侧,那么是_________.2.最值的概念一般地,设函数的定义域为,(1)如果存在,使得对于任意的,都有,那么称为的最大值。(2)如果存在,使得对于任意的,都有,那么称为的最小值。【复习回顾】1.函数的单调增区间是_____________.2.函数的极大值是_______________.3.函数在上的值域为______________.4.函数的值域为________________.【典例精析】例1:已知函数在处取得极值.(1)求的值;(2)若有极大值28,求在上的最小值。小结三次函数图像的特点:三次函数,导函数为,其中,请填下表特别注意:可导函数()yfx在0xx处取得极值是0'()0fx的充分不必要条件.例3:已知函数,有两个零点,求的取值范围。导函数图yxx2x1OyxOx0yxOx0原函数图象单调区间极值跟踪训练:1.做出下列函数的草图:(1)(2)(3)2..函数在上恒成立,求实数的范围。例3.讨论函数在区间上的最大值。跟踪训练:函数在的最小值为3,求实数的值。