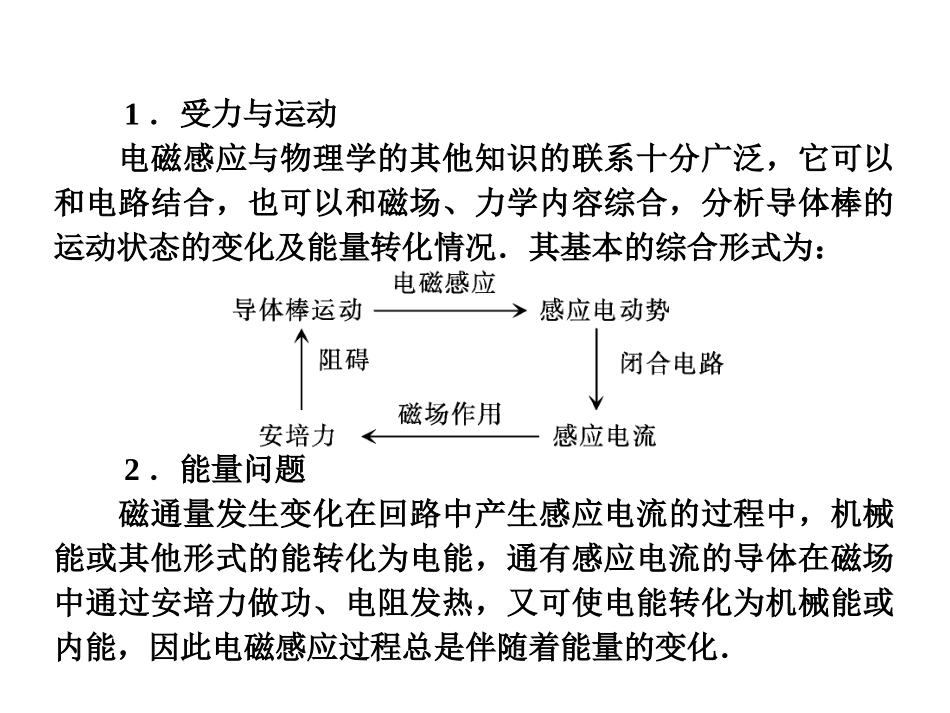
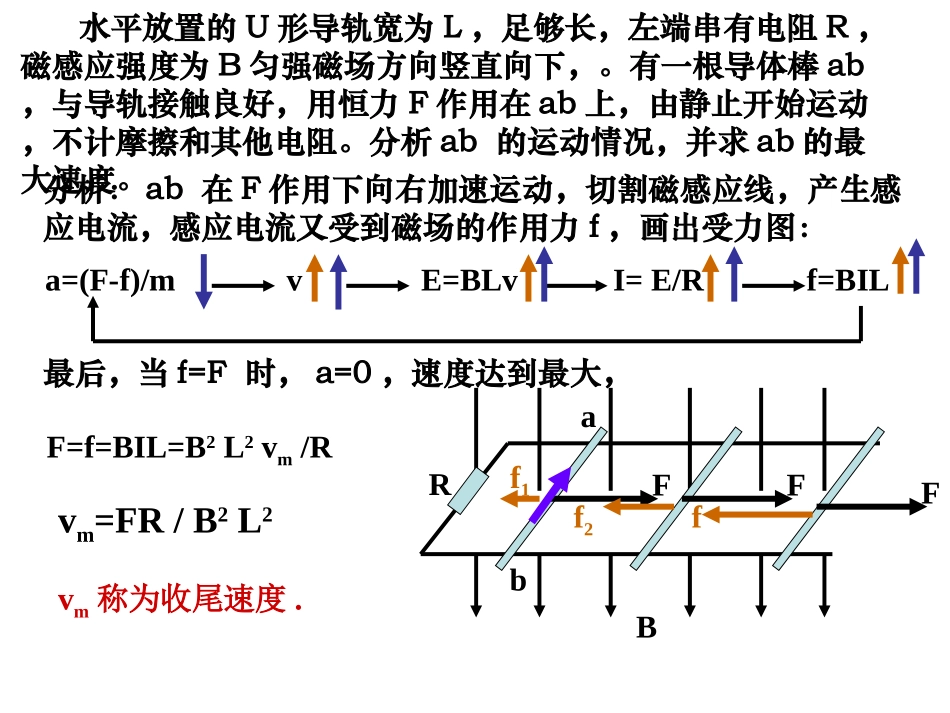
电磁感应中的动力学问题电磁感应中的动力学问题电磁感应中产生的感应电流在磁场中将受到安培力的作用,因此,电磁感应问题往往跟力学问题联系在一起。解决这类电磁感应中的力学问题,不仅要应用电磁学中的有关规律,如楞次定律、法拉第电磁感应定律、左右手定则、安培力的计算公式等,还要应用力学中的有关规律,如牛顿运动定律、动能定理、机械能守恒定律等。要将电磁学和力学的知识综合起来应用。由于安培力和导体中的电流、运动速度均有关,所以对磁场中运动导体进行动态分析十分必要。1.受力与运动电磁感应与物理学的其他知识的联系十分广泛,它可以和电路结合,也可以和磁场、力学内容综合,分析导体棒的运动状态的变化及能量转化情况.其基本的综合形式为:2.能量问题磁通量发生变化在回路中产生感应电流的过程中,机械能或其他形式的能转化为电能,通有感应电流的导体在磁场中通过安培力做功、电阻发热,又可使电能转化为机械能或内能,因此电磁感应过程总是伴随着能量的变化.水平放置的U形导轨宽为L,足够长,左端串有电阻R,磁感应强度为B匀强磁场方向竖直向下,。有一根导体棒ab,与导轨接触良好,用恒力F作用在ab上,由静止开始运动,不计摩擦和其他电阻。分析ab的运动情况,并求ab的最大速度。abBRF分析:ab在F作用下向右加速运动,切割磁感应线,产生感应电流,感应电流又受到磁场的作用力f,画出受力图:f1a=(F-f)/mvE=BLvI=E/Rf=BILFf2最后,当f=F时,a=0,速度达到最大,FfF=f=BIL=B2L2vm/Rvm=FR/B2L2vm称为收尾速度.如图所示,在一均匀磁场中有一U形导线框abcd,线框处于水平面内,磁场与线框平面垂直,R为一电阻,ef为垂直于ab的一根导体杆,它可在ab、cd上无摩擦地滑动。杆ef及线框中导线的电阻都可不计。开始时,给ef一个向右的初速度,则()A.ef将减速向右运动,但不是匀减速B.ef将匀减速向右运动,最后停止C.ef将匀速向右运动D.ef将往返运动RedcabfA竖直放置的U形导轨宽为L,上端串有电阻R。磁感应强度为B的匀强磁场方向垂直于纸面向外。金属棒ab的质量为m,与导轨接触良好,不计摩擦。从静止释放后ab保持水平而下滑。试分析ab下滑过程中的运动情况并确定能表征其最终运动情况的物理量的值.(其余导体部分的电阻都忽略不计)基本思路是:F=BIL临界状态v与a方向关系运动状态的分析a变化情况F=ma合外力运动导体所受的安培力感应电流确定电源(Er)rREI如图所示,竖直平行导轨间距l=20cm,导轨顶端接有一电键K。导体棒ab与导轨接触良好且无摩擦,ab的电阻R=0.4Ω,质量m=10g,导轨的电阻不计,整个装置处在与轨道平面垂直的匀强磁场中,磁感强度B=1T。当ab棒由静止释放0.8s后,突然接通电键,不计空气阻力,设导轨足够长。求ab棒的最大速度和最终速度的大小。(g取10m/s2)Kab解:mgRvlBm22ab棒由静止开始自由下落v=gt=8m/s则闭合K瞬间I=Blv/R=4Aab棒受重力mg=0.1N,安培力F=BIL=0.8N.因为F>mg,ab棒加速度向上,开始做减速运动,产生的感应电流和受到的安培力逐渐减小,当安培力F′=mg时,开始做匀速直线运动。此时满足B2l2vm/R=mg解得最终速度,vm=mgR/B2l2=1m/s。闭合电键时速度最大为8m/s。t=0.8sl=20cmR=0.4Ωm=10gB=1TKabmgF竖直放置冂形金属框架,宽1m,足够长,一根质量是0.1kg,电阻0.1Ω的金属杆可沿框架无摩擦地滑动.框架下部有一垂直框架平面的匀强磁场,磁感应强度是0.1T,金属杆MN自磁场边界上方0.8m处由静止释放(如图).求:(1)金属杆刚进入磁场时的感应电动势;(2)金属杆刚进入磁场时的加速度;(3)金属杆运动的最大速度答:(1)smghv/42(2)I=E/R=4AF=BIL=0.4Na=(mg-F)/m=6m/s2;(3)F=BIL=B2L2vm/R=mgvm=mgR/B2L2=10m/s,E=BLv=0.4V;NM如图所示,两足够长的光滑金属导轨竖直放置,相距为L,一理想电流表与两导轨相连,匀强磁场与导轨平面垂直。一质量为m、有效电阻为R的导体棒在距磁场上边界h处静止释放。导体棒进入磁场后,流经电流表的电流逐渐减小,最终稳定为I。整个运动过程中,导体棒与导轨接触良好,且始终保持水平,不计导轨和电流表的电阻。求:(1)磁感应强度B的大小;(2)电流稳定后,导体棒运动速度v的大小;(3)流经...