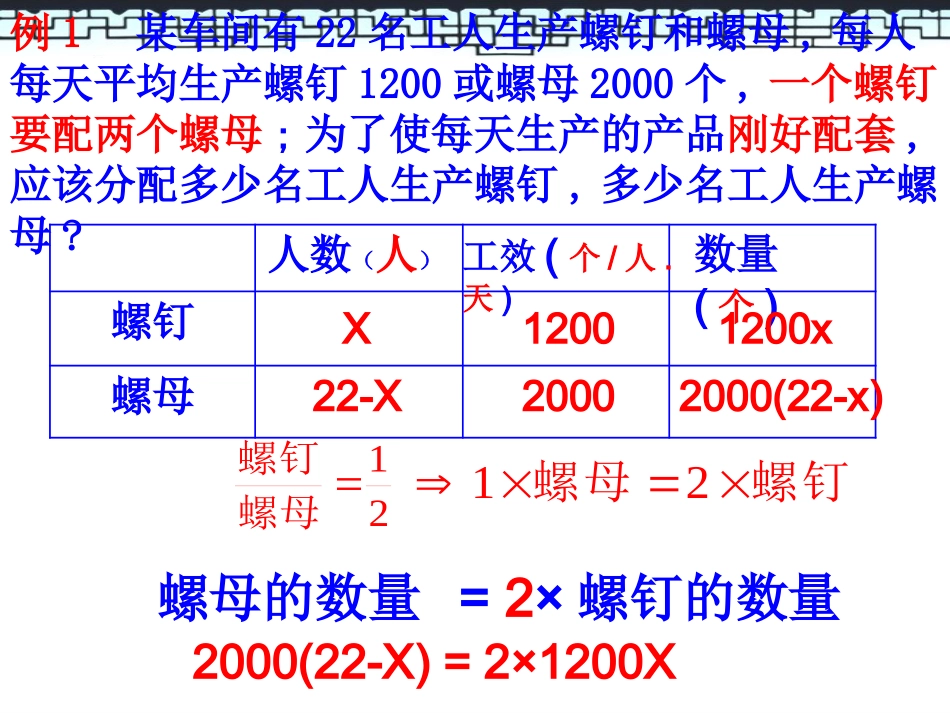
3.4实际问题与一元一次方程第一课时调配问题学习目标会用一元一次方程解决“配套”类型问题在实际问题中,大家常见到一些配套组合问题,如螺钉与螺母的配套,盒身与盒底的配套等。解决这类问题的方法是:抓住配套关系,设出未知数,根据配套关系列出方程,通过解方程来解决问题。例1某车间有22名工人生产螺钉和螺母,每人每天平均生产螺钉1200或螺母2000个,一个螺钉要配两个螺母;为了使每天生产的产品刚好配套,应该分配多少名工人生产螺钉,多少名工人生产螺母?2000(22-X)=2×1200X21螺母螺钉螺钉螺母21螺钉螺母人数(人)工效(个/人.天)数量(个)X22-X120020001200x2000(22-x)螺母的数量=2×螺钉的数量解:设分配x名工人生产螺钉,则生产螺母的人数为(22-x)人.依题意,得:去括号,得44000-2000x=2400x移项,得-2000x-2400x=-44000合并同类项,得-4400x=-44000系数化为1,得x=10.所以生产螺母的人数为:22-x=12(人).答:分配10人生产螺钉,12人生产螺母.可使每天生产的产品刚好配套。2000(22-X)=2×1200X问题问题33:以上问题还有其他的解决方法吗?:以上问题还有其他的解决方法吗?二、应用与探究二、应用与探究例如:例如:解:设应安排解:设应安排xx名工人生产螺母,名工人生产螺母,((2222--xx))名工人生产螺钉名工人生产螺钉..依题意得:依题意得:2×12002×1200((2222--xx))==22000000x.x.(1)一个服装车间,共有90人,每人每小时加工1件衣服或2条裤子,问怎样安排工作才能使衣服和裤子正好配套?(一件衣服配一条裤子)练一练衣服裤子人数(人)工效(件/人.h)数量(件)X90-X12x2(90-x)X=2(90-X)11裤子衣服衣服的数量=裤子的数量裤子衣服11解:设做衣服人数为x人,则做裤子的人数为(90-x)人.依题意,得:x=2(90-x)去括号,得x=180-2x移项,得x+2x=180合并同类项,得3x=180系数化为1,得x=60.所以做裤子的人数为:90-x=30(人).答:做衣服的人数为60人,做裤子的人数为30人.(2)某水利工地派40人去挖土和运土,如果每人每天平均挖土5方或运土3方,那么应怎样安排人员,正好能使挖出的土及时运走?挖土运土人数(人)工效(方/人.天)数量(方)X40-X535x3(40-x)5X=3(40-X)挖土的数量=运土的数量(2)某水利工地派40人去挖土和运土,如果每人每天平均挖土5方或运土3方,那么应怎样安排人员,正好能使挖出的土及时运走?解:设每天派x人挖土,依题意,得:5x=3(40-x)解得:x=15所以每天运土人数为:40-x=25(人)答:每天派15人挖土,25人运土,正好能使挖出的土及时运走.方法规律:生产调配问题通常从调配后各量之间的倍、分关系寻找相等关系,建立方程。归纳小结:用一元一次方程解决实际问题的基本过程如下:实际问题设未知数,列方程一元一次方程实际问题的答案解方程一元一次方程的解(x=a)检验这一过程包括设、列、解、检、答等步骤,即设未知数,列方程,解方程,检验所得结果,确定答案。正确分析问题中的相等关系是列方程的基础。作业11、必做题:基础训练、必做题:基础训练7272页页课堂练习课堂练习11、、33题题课后训练课后训练11、、22题题22、、选做题:选做题:7373页页33、、44题题