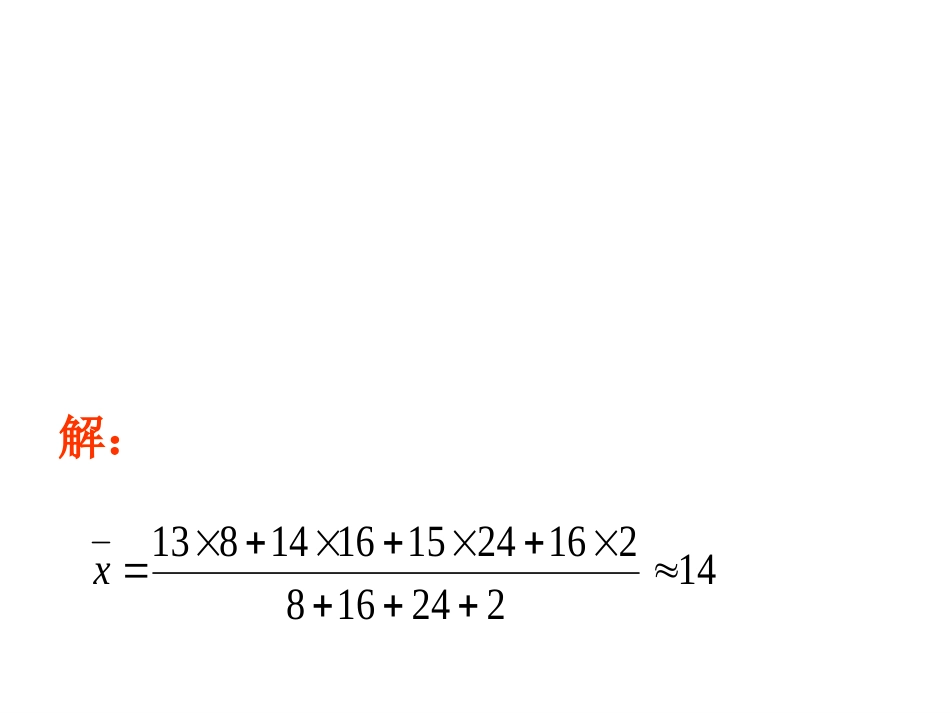人教版八年级(下册)20.1数据的集中趋势(第2课时)第二十章数据的分析问题:某跳水队为了解运动员的年龄情况,作了一次年龄调查,结果如下:13岁8人,14岁16人,15岁24人,16岁2人。求这个跳水队运动员的平均年龄(结果取整数)。解:这个跳水队运动员的平均年龄为:1422416821624151614813x(岁)在求n个数的算术平均数时,如果x1出现f1次,x2出现f2次,…,xk出现fk次(这里f1+f2+…+fk=n)那么这n个数的算术平均数也叫做x1,x2,…,xk这k个数的加权平均数,其中f1,f2,…,fk分别叫做x1,x2,…,xk的权。例1、为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,得到下表:载客量/人组中值频数(班次)1≤x<2111321≤x<4131541≤x<61512061≤x<81712281≤x<1019118101≤x<12111115这天5路公共汽车平均每班的载客量是多少?根据上面的频数分布表求加权平均数时,统计中常用的各组的组中值代表各组的实际数据,把各组频数看作相应组中值的权。载客量/人组中值频数(班次)1≤x<2111321≤x<4131541≤x<61512061≤x<81712281≤x<1019118101≤x<12111115由此这天5路公共汽车平均每班的载客量是:)(731518222015315111189122712051531311人x载客量/人组中值频数(班次)1≤x<2111321≤x<4131541≤x<61512061≤x<81712281≤x<1019118101≤x<12111115组中值是指数据分组后,每一个小组的两个端点的数的平均数。例如,小组1≤x<21的组中值为组中值11的权是它的频数3,112211从表中,你能知道这一天5路公共汽车大约有多少班次的载客量在平均载客量以上吗?占全天总班次的百分比是多少?由表格可知,81≤x<101的18个班次和101≤x<121的15个班次共有33个班次超过平均载客量,占全天总班次的百分比为33/83等于39.8%载客量/人组中值频数(班次)1≤x<2111321≤x<4131541≤x<61512061≤x<81712281≤x<1019118101≤x<12111115?思考例某灯泡厂为测量一批灯泡的使用寿命,从中抽查了100只灯泡,它们的使用寿命如下表所示:这批灯泡的平均使用寿命是多少?使用寿命x(单位:时)600≤x<10001000≤x<14001400≤x<18001800≤x<22002200≤x<2600灯泡数(单位:个)1019253412分析:抽出的100只灯泡的使用寿命组成一个样本,可以利用样本的平均使用寿命来估计这批灯泡的平均使用寿命。解:根据表格,可以得出各小组的组中值,于是10012240034200025160019120012800x即样本平均数为1676.由此可以估计这批灯泡的平均使用寿命大约是1676小时。=1676=1676使用计算器说明,操作时需要参阅计算器的使用说明书,通常需要先按动有关键,使计算器进入统计状态;然后依次输入数据x1,x2,…,xn,以及它们的权f1,f2,…,fn;最后按动求平均数的功能键(例如键),计算器便会求出平均数的值x练习1、下表是校女子排球队队员的年龄分布:年龄13141516频数1452求校女子排球队队员的平均年龄)(7.142541216515414113岁x答:校女子排球队队员的平均年龄为14.7岁.解:02468101214405060708090频数周长/cm2、为了绿化环境,柳荫街引进一批法国梧桐,三年后这些树的树干的周长情况如图所示,计算这批法国梧桐树干的平均周长(精确到0.1cm)答:这批梧桐树干的平均周长是63.8cm6101412865.8105.7145.6125.585.4x=63.8(cm)问题1:求加权平均数的公式是什么?nnnxxx3212211nfxfxfxxkk2211在求n个数的算术平均数时,如果x1出现f1次,x2出现f2次,…,xk出现fk次(这里f1+f2+…+fk=n)那么这n个数的算术平均数nxxx,,,21n,,,21若n个数的权分别是则:叫做这n个数的加权平均数。也叫做k个数的加权平均数问题2:你如何理解加权平均数中的权的意思?问题3:当要考察的对象很多或考察本身带有破坏性时,统计学中常常使用什么方法获得对总体认识?数据的权能够反映的数据的相对“重要程度”。常常用样本数据的代表意义来估计总体例如:实际生...