一元二次不等式的解法第一课时VIP免费

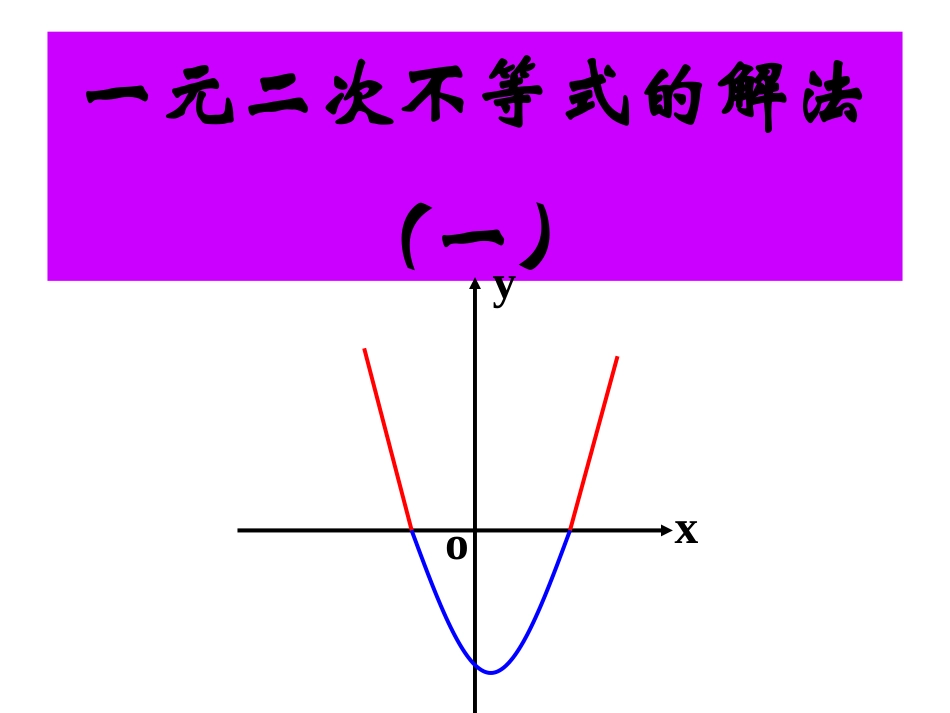
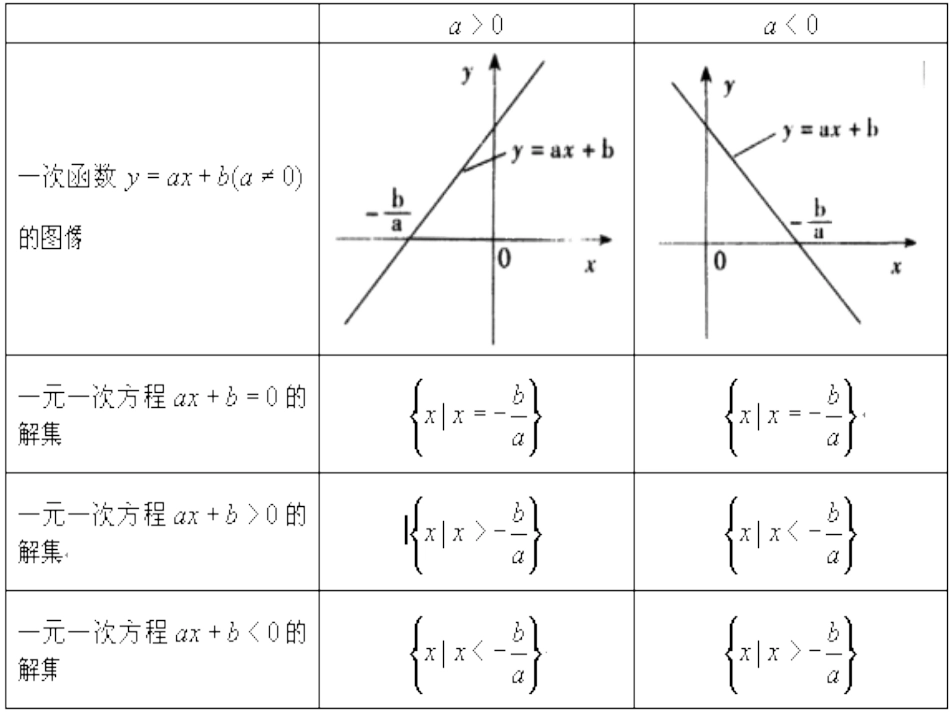
一元二次不等式的解法（一）oxy一复习引入问题1:同学们在初中学习过一元一次不等式的解法,你能说出一元一次函数，一元一次方程，一元一次不等式之间的关系吗?能通过观察一次函数的图像求得一元一次不等式的解集吗？一元一次函数，一元一次方程，一元一次不等式之间的关系,如下图:问题：（1）如何解一元二次方程（2）二次函数的图象是什么曲线？（3）一元二次方程的解与二次函数的图象有什么联系？)0(02acbxax)0(2acbxaxy)0(02acbxax)0(2acbxaxy•画出下列函数的图象•（1）y=x2+x-6•(2)y=x2+2x+1•(3)y=x2+x+1•观察图象并回答•当x取什么值时？y>0•当x取什么值时？y=0•当x取什么值时？y<0一元二次方程的解实际上就是二次函数与x轴交点的横坐标。)0(02acbxax)0(2acbxaxy下面我们来研究如何应用二次函数的图象来解一元二次不等式。首先，我们可以把任何一个一元二次不等式转化为下列四种形式中的一种：)0(0)1(2acbxax)0(0)2(2acbxax)0(0)3(2acbxax)0(0)4(2acbxax以上四个不等式中我们规定了如果题目中给出的不等式中二次项系数小于0，哪怎么办呢？0a对了，我们只要在不等式两边同乘-1，然后把不等式的方向改变一下，就可化为以上四种形式中的一种。下面我们就利用二次函数的图象来解以上4个不等式。设f(x)=ax2+bx+c(a＞0),且设方程f(x)=0在△＞0时的两个根分别是x1、x2，且x1＜x2。下面我们一起来完成下表：△＝b2－4ac△＞0△＝0△＜0f(x)＞0的解集f(x)＜0的解集f(x)≥0的解集f(x)≤0的解集y=f(x)的图象Oxyx1x212xxxxx或21xxxx12xxxxx或21xxxxOxyx＝－b／2aabxRx2abxx2OxyRRR填写上表的依据是二次函数的图象，这实际上是一种数形结合的思想。由此我们可以得出解一元二次不等式的一般步骤：（1）把所给不等式化为四种标准形式之一；（2）判断所对应二次方程的根的情况；若有根，则求出其根。（3）画出所对应的二次函数的图象；（4）根据图象写出不等式的解集。例1、求下列不等式的解集：0156)1(2xx01544)2(2xx325)3(2xx169)4(2xxxx453)5(2解：（1）将原不等式变形为：即∴原不等式的解集为01562xx0)1)(16(xx611xxx或解：（2）将原不等式变形为∴原不等式的解集为0)32)(52(xx2325xx解：（3）将原不等式变形为 方程所对应的⊿=-56＜0∴原不等式的解集为R。03252xx03252xx解：（4）将原不等式变形为 所对应的二次方程的⊿=0，∴原不等式的解集为01692xx31xRx解：（5）将原不等式变形为 所对应的二次方程的⊿=-44＜0，∴原不等式的解集为05432xx例2、已知关于x的不等式的解集是{x︱x＜-2或x＞}求的解集。02cbxax2102cbxax分析：本题主要强化一元二次方程、一元二次不等式与二次函数图象间的关系。解法一：由此可得abc=(-2)(-5)(-2)且a<0,∴所求解的不等式为：0)21)(2(212xxxxxx或0252{025222xxxxxx02522xx即(x-2)(2x-1)<0,解得∴不等式的解集为221x02cbxax221xx解法二：由已知得的两个根，且a＜0，∴解得021,22cbxax是方程02141024cbacbaacab,25∴不等式即为∴即不等式的解集为02cbxax02522xx221x02cbxax221xx小结：两种解法都是先试图找出a、b、c的关系，再解出一元二次不等式的解集。例3、不等式对任意xR∈恒成立，求a与m之间的关系。)1()1(22xxmaaxxa分析：不等式对任意xR∈恒成立，就是不等式的解集为R。对于二次不等式的解集为R的条件为02cbxax0402acba解：将原不等式变形为以上不等式对xR∈恒成立。当a-m+1=0时，原不等式化为–x-1＞0，与xR∈不符，应舍去。0)()()1(2maxmaxma当a-m+1≠0时，由②得：∴a＞m，则...