抛物线及其标准方程 (2)VIP免费

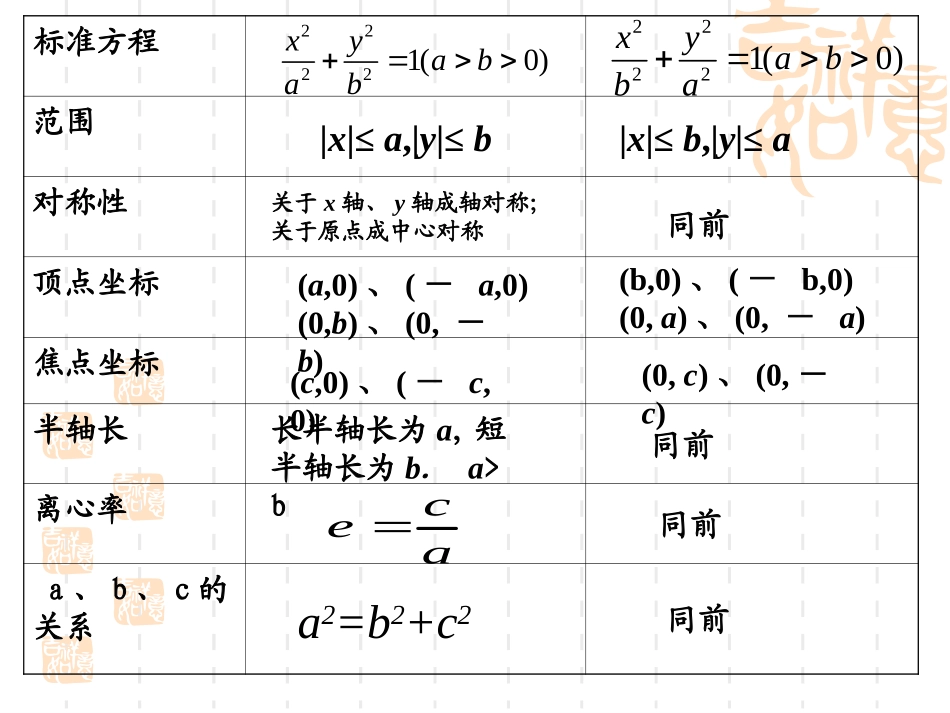
标准方程范围对称性顶点坐标焦点坐标半轴长离心率a、b、c的关系22221(0)xyabab关于x轴、y轴成轴对称；关于原点成中心对称长半轴长为a,短半轴长为b.a>bceaa2=b2+c222221(0)xyabba同前(b,0)、(－b,0)(0,a)、(0,－a)同前同前同前|x|≤a,|y|≤b|x|≤b,|y|≤a(a,0)、(－a,0)(0,b)、(0,－b)(c,0)、(－c,0)(0,c)、(0,－c)关于x轴、y轴、原点对称图形方程范围对称性顶点离心率)0(1babyax2222A1（-a，0），A2（a，0）A1（0，-a），A2（0，a）),b(abxay0012222Rxayay，或关于x轴、y轴、原点对称)1(eace渐进线xbay..yB2A1A2B1xOF2F1xB1yO.F2F1B2A1A2.F1(-c,0)F2(c,0)F2(0,c)F1(0,-c)Ryaxax，或)1(eacexaby生活中的抛物线美丽的赵州桥生活中的抛物线生活中的抛物线抛球运动返回目录返回目录请同学们准备以下工具,两个同学分工协作,按下列方法画出动点轨迹.1.在纸一侧固定直尺2.将直角三角板的一条直角边紧贴直尺3.取长等于另一直角边长的绳子4.固定绳子一端在直尺外一点6.用笔将绳子拉紧,并使绳子紧贴三角板的直角边5.固定绳子另一端在三角板顶点A上7.上下移动三角板,用笔画出轨迹A展示课前实践作业动画演示返回目录返回目录抛物线的画法抛物线的画法数学这门学科不仅需要观察，还需要实验数学这门学科不仅需要观察，还需要实验一、抛物线的定义:M·Fl·在平面内,与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫抛物线.点F叫抛物线的焦点,直线l叫抛物线的准线.d为M到l的距离准线焦点dH即:若,则点M的轨迹是抛物线.1dMF2.比较椭圆、双曲线标准方程的建立过程，你认为如何选择坐标系,建立的抛物线的方程才能更简单?1.若l经过点F,动点M的轨迹是什么?返回目录返回目录求曲线方程的基本步骤是怎样的？化简列式设点建系M·Fl·H二、抛物线标准方程的推导二、抛物线标准方程的推导化简列式设点建系解：以过F且垂直于直线l的直线为x轴,垂足为K.以F,K的中点O为坐标原点建立直角坐标系xoy.两边平方,整理得xKyOF），设0(p＞pFK，dMFMP．），准线的方程为，的坐标为（则焦点202pxpFMl···（x,y）设M（x，y）是抛物线上任意一点，H点M到l的距离为d．d由抛物线的定义，抛物线就是点的集合2222pxypx所以）0(22p＞pxy二、抛物线标准方程的推导二、抛物线标准方程的推导返回目录返回目录三、抛物线的标准方程y2=2px（p＞0）其中pp为正常数，它的几何意义是:焦点到准线的距离．y2=2px（p＞0）方程y2=2px（p＞0）表示焦点在x轴正半轴上的抛物线．．的方程为），准线，（的坐标为焦点2:02:pxlpFxKyOFMl···Hd返回目录返回目录三、抛物线的标准方程抛物线的标准方程还有哪些不同形式?若抛物线的开口分别朝左、朝上、朝下，你能根据上述办法求出它的标准方程吗？探探究究各组分别求解开口不同时抛物线的标准方程。三、抛物线的标准方程的其他形式OyxFMlN··FMlN··HFMlN··FMlN··xHypxy220ppxy220ppyx220ppyx220p0,2p2px0,2p2px2,0p2py2,0p2py如何确定抛物线焦点位置及开口方向?一次变量定焦点开口方向看正负图形图形标准方程标准方程焦点坐标焦点坐标准线方程准线方程xHFOMlyxyHFOMlxyHFOMlxyHFOMl返回目录返回目录4.M是抛物线y2=4x上一点，若点M到焦点F的距离等于6，求点M坐标.3.焦点在x轴负半轴，且焦点到准线距离;2四、抛物线及其标准方程的应用yx82yx162)52,5(M根据下列条件求抛物线的标准方程？xy2221.抛物线的焦点坐标是F(0,-2);2.抛物线的准线方程是y=-4;．．焦点到准线的距离为23．或或或yxyxxyxy222222222222返回目录返回目录xyF(0,-2)Ol．是所求抛物线的标准方程，所以，轴负半轴上，且在），，标为（．因为抛物线的焦点坐yxpy8222012xyFOly=-4．方程是所以所求抛物线的标准，＝轴上，且所以焦点在ｙ轴的正半，程是．因为抛物线的准线方yxpy1642422返回例1返回目录返回目录xHFOMlyxyFOl．方程为求抛物线的标准的负半轴...