双曲线标准方程111VIP免费

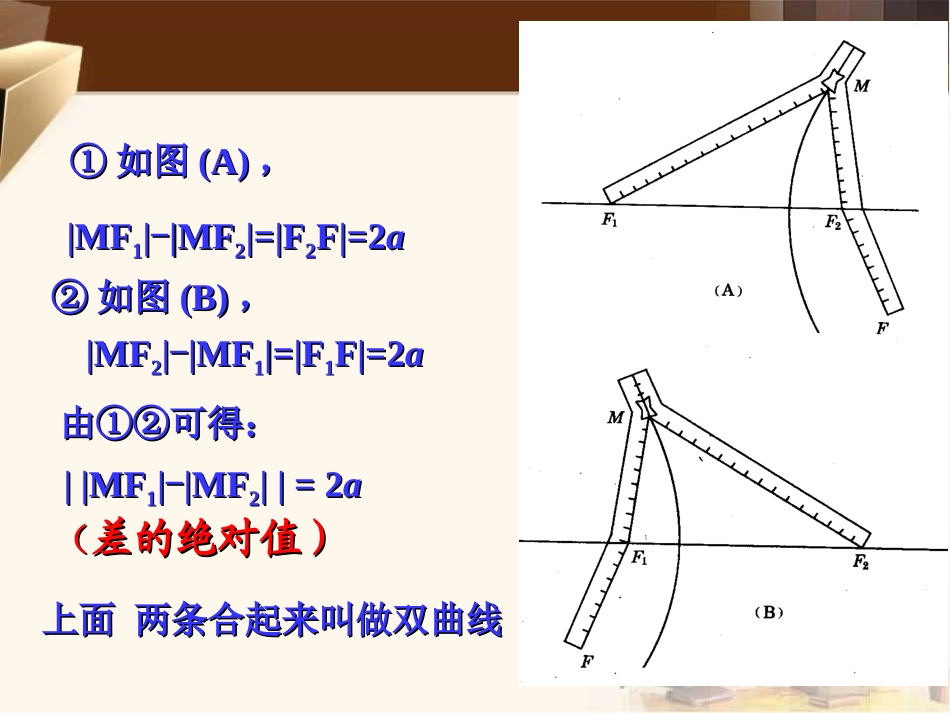
双曲线及其标准方程1.椭圆的定义和等于常数2a(2a>|F1F2|>0)的点的轨迹.平面内与两定点F1、F2的距离的1F2F0,c0,cXYOyxM,2.引入问题：差等于常数的点的轨迹是什么呢？平面内与两定点F1、F2的距离的复习双曲线图象拉链画双曲线|MF1|+|MF2|=2a(2a>|F1F2|>0)①①如图如图(A)(A)，，|MF|MF11||--|MF|MF22|=|F|=|F22F|=2F|=2aa②②如图如图(B)(B)，，上面两条合起来叫做双曲线上面两条合起来叫做双曲线由①②可得：由①②可得：||MF||MF11||--|MF|MF22||=2||=2aa（（差的绝对值）差的绝对值）|MF|MF22||--|MF|MF11|=|F|=|F11F|=2F|=2aa①两个定点F1、F2——双曲线的焦点;②|F1F2|=2c——焦距.（1）2a<2c；oF2F1M平面内与两个定点F1，F2的距离的差的绝对值等于常数（小于︱F1F2︱)的点的轨迹叫做双曲线.（2）2a>0；双曲线定义思考：（1）若2a=2c,则轨迹是什么？（2）若2a>2c,则轨迹是什么？说明（3）若2a=0,则轨迹是什么？||MF1|-|MF2||=2a(1)两条射线(2)不表示任何轨迹(3)(3)线段线段FF11FF22的垂直平分线的垂直平分线F2F1MxOy求曲线方程的步骤：双曲线的标准方程1.建系.以F1,F2所在的直线为x轴，线段F1F2的中点为原点建立直角坐标系2.设点．设M（x,y）,则F1(-c,0),F2(c,0)3.列式|MF1|-|MF2|=±2a4.化简aycxycx2)()(2222即aycxycx2)()(2222222222)(2)(ycxaycx222)(ycxaacx)()(22222222acayaxac222bac)0,0(12222babyax此即为焦点在x轴上的双曲线的标准方程12222byax12222bxayF2F1MxOyOMF2F1xy)00(ba，若建系时,焦点在y轴上呢?定义方程焦点a.b.c的关系F（±c，0）F（±c，0）a>0，b>0，但a不一定大于b，c2=a2+b2a>b>0，a2=b2+c2双曲线与椭圆之间的区别与联系双曲线与椭圆之间的区别与联系||MF1|－|MF2||=2a|MF1|+|MF2|=2a椭圆双曲线F（0，±c）F（0，±c）22221(0)xyabab22221(0)yxabab22221(0,0)xyabab22221(0,0)yxabab解：∴126PFPF∵焦点为12(5,0),(5,0)FF∴可设所求方程为:22221xyab(a>0,b>0).∵2a=6,2c=10,∴a=3,c=5.所以点P的轨迹方程为221916xy.∵1210FF>6,由双曲线的定义可知，点P的轨迹是一条双曲线,例1：已知两定点1(5,0)F,2(5,0)F,动点P满足126PFPF,求动点P的轨迹方程.变式训练1:已知两定点1(5,0)F,2(5,0)F,动点P满足1210PFPF,求动点P的轨迹方程.解：∴1210PFPF轨迹方程为0(55)yxx或≥≤.∵1210FF,点P的轨迹是两条射线,变式训练2:已知两定点1(5,0)F,2(5,0)F,动点P满足126PFPF,求动点P的轨迹方程.变式2答案变式训练2:已知两定点1(5,0)F,2(5,0)F,动点P满足126PFPF,求动点P的轨迹方程.解：∴126PFPF∵焦点为12(5,0),(5,0)FF∴可设双曲线方程为:22221xyab(a>0,b>0).∵2a=6,2c=10,∴a=3,c=5.∴b2=52－32=16.所以点P的轨迹方程为221916xy(3)≥x.∵1210FF>6,由双曲线的定义可知，点P的轨迹是双曲线的一支(右支),例2:如果方程表示双曲线，求m的取值范围.22121xymm解:方程表示焦点方程表示焦点在在yy轴双曲线时，轴双曲线时，则则mm的取值范围的取值范围_____________._____________.22121xymm思考：21mm得或(2)(1)0mm由2m∴m的取值范围为(,2)(1,)学习小结:本节课主要是进一步了解双曲线的定义及其标准方程,并运用双曲线的定义及其标准方程解决问题,体会双曲线在实际生活中的一个重要应用.其实全球定位系统就是根据例2这个原理来定位的.运用定义及现成的模型思考,这是一个相当不错的思考方向.即把不熟悉的问题往熟悉的方向转化,定义模型是最原始,也是最容易想到的地方.看前的系数，哪一个为正，则在哪一个轴上22,yx双曲线的标准方程与椭圆的标准方程有何区别与双曲线的标准方程与椭圆的标准方程有何区别与联系联系??如何判断双曲线的焦点在哪个轴上？如何判断双曲线的焦点在哪个轴上？