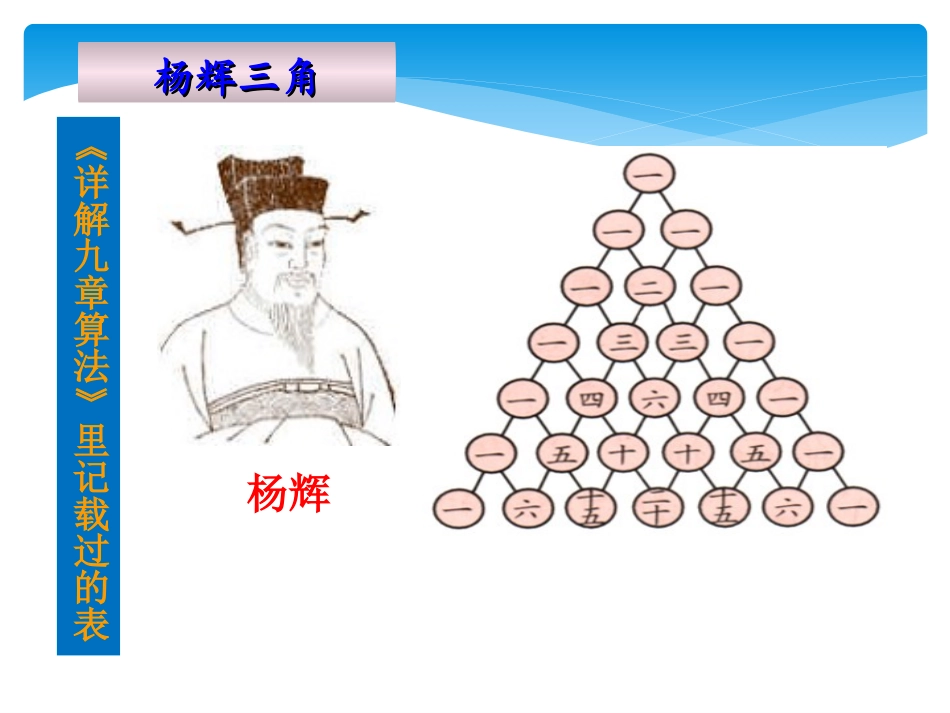
人教版六年级上册襄阳市第二十三中学周海荣数与形数学广角三角形的两条斜边上都是数字1,而其余的数都等于它肩上的两个数字相加。杨辉三角杨辉三角《详解九章算法》里记载过的表杨辉我国北宋数学家贾宪(约公元11世纪)已经用过“杨辉三角”,这表明我国发现这个表不晚于11世纪。在欧洲,这个表被认为是法国数学家物理学家帕斯卡首先发现的,他们把这个表叫做帕斯卡三角。杨辉三角的发现要比欧洲早500年左右。中国古代数学史曾经有自己光辉灿烂的篇章,而杨辉三角的发现就是十分精彩的一页。这样一个三角在我们的数学学习中最简单的就是叫找规律。以后我们要学的二项式定理与杨辉三角形是一对天然的数形趣遇,它把数形结合带进了计算数学。今天我们就一起来走进奇妙无穷的数学广角------数与形11+3观察一下,下面三幅图中分别有多少个小正方形?用平方数表示分别是多少?探究新知探究新知例例11212=22=31+3+5===再观察,从左边图1到图2再到图3,依次增加了多少个小正方形?如果用加法算式怎么表示?49小组合作:动手用小正方形摆出1+3和1+3+5表示的图形,并根据图形和算式讨论,它们有什么关系?1+3+5=()231+3=()22()11=2想一想:算式中的加数在图中的什么地方?平方数代表的又是图中的什么?1+3+5=()231+3=()22()11=2左边的加数是大正方形右上角的小正方形和其他“L”形图形所包含的小正方形个数之和。右边正好是每行或每列小正方形个数的平方。从1开始的几个连续奇数相加,和即是几的平方。如果继续这样摆下去,第4个、第5个大正方形各需要几个小正方形?1+3+5+7=16=421+3+5+7+9=25=52由于数量为1、4、9、16、25……的小正方形可以组成一个大正方形,这些数也叫做“正方形数”。1+3+5+7=()1+3+5+7+9+11+13=()1.你能利用规律直接写一写吗?471+3+5+7+9+11+13+15+17=9222运用知识运用知识从1开始的几个连续奇数相加,和即是几的平方。2.你能利用规律快速判断吗?运用知识运用知识1+2+3+4+5=525+7+9=321+3+5+7+9+11+13+15=64(×)(×)(√)1+2+3+4+5+6+7+8=82(×)1+3+5+7+5+3+1=()3.请根据例1的结论算一算。25可以看成两部分:1+3+5+7=425+3+1=3242+32=25运用知识运用知识1+3+5+7+9+11+13+11+9+7+5+3+1=()853.请根据例1的结论算一算。运用知识运用知识1+3+5+7+5+3+1=(25)31610根据图形与数的规律接着画一画,填一填。1521如果不画,这样列下去,第十个数是多少?数缺形时少直观,形少数时难入微,数形结合百般好,割裂分家万事休。——华罗庚总结:通过这节课的学习,你有哪些收获愿意和我们大家一起分享一下呢?拓展延伸运用例1学到的思考方法,能直接算出下面式子的结果吗?2+4+6+8+10+12+14+16+18+20=()规律:从2开始的n个连续偶数的和等于。