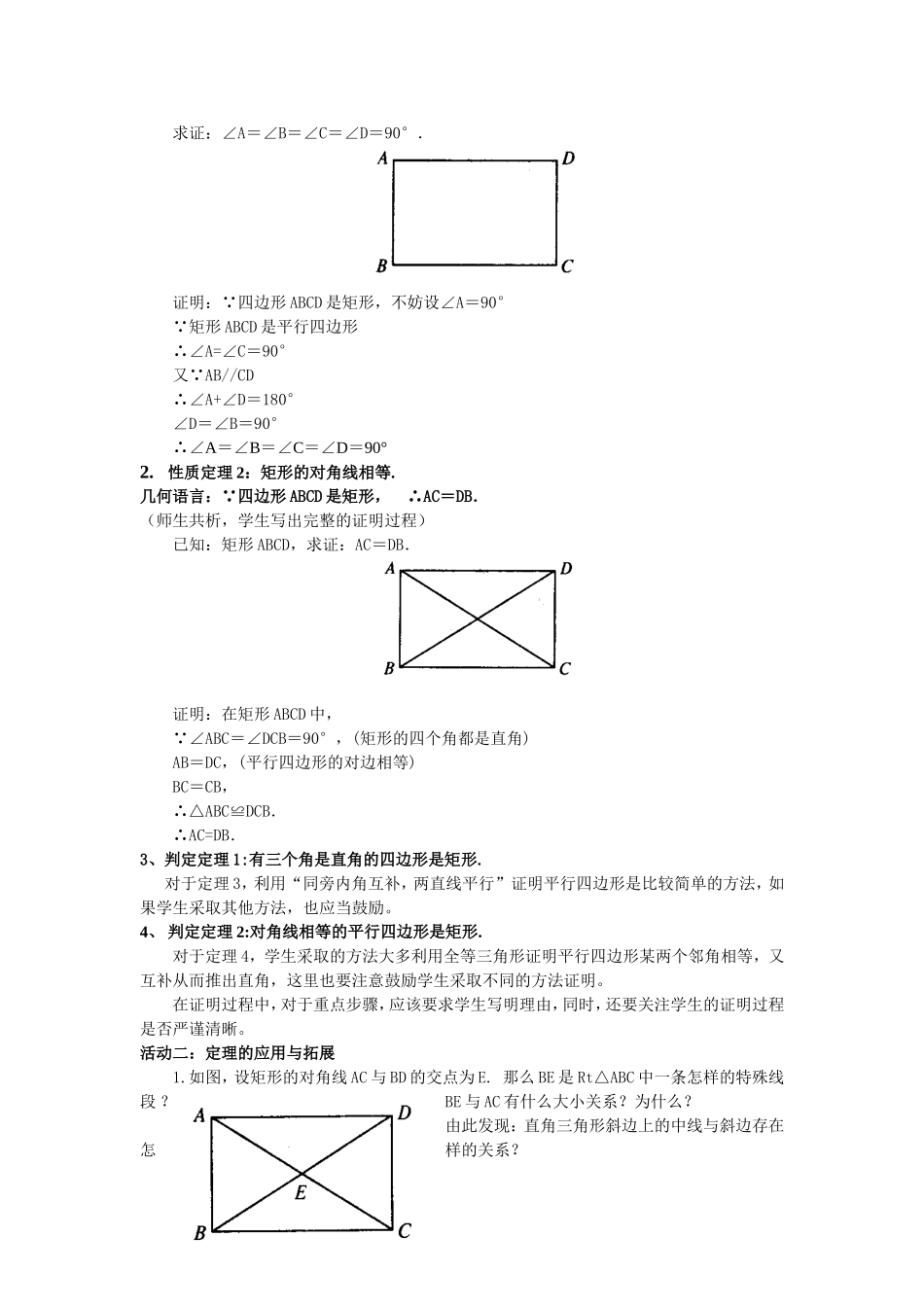
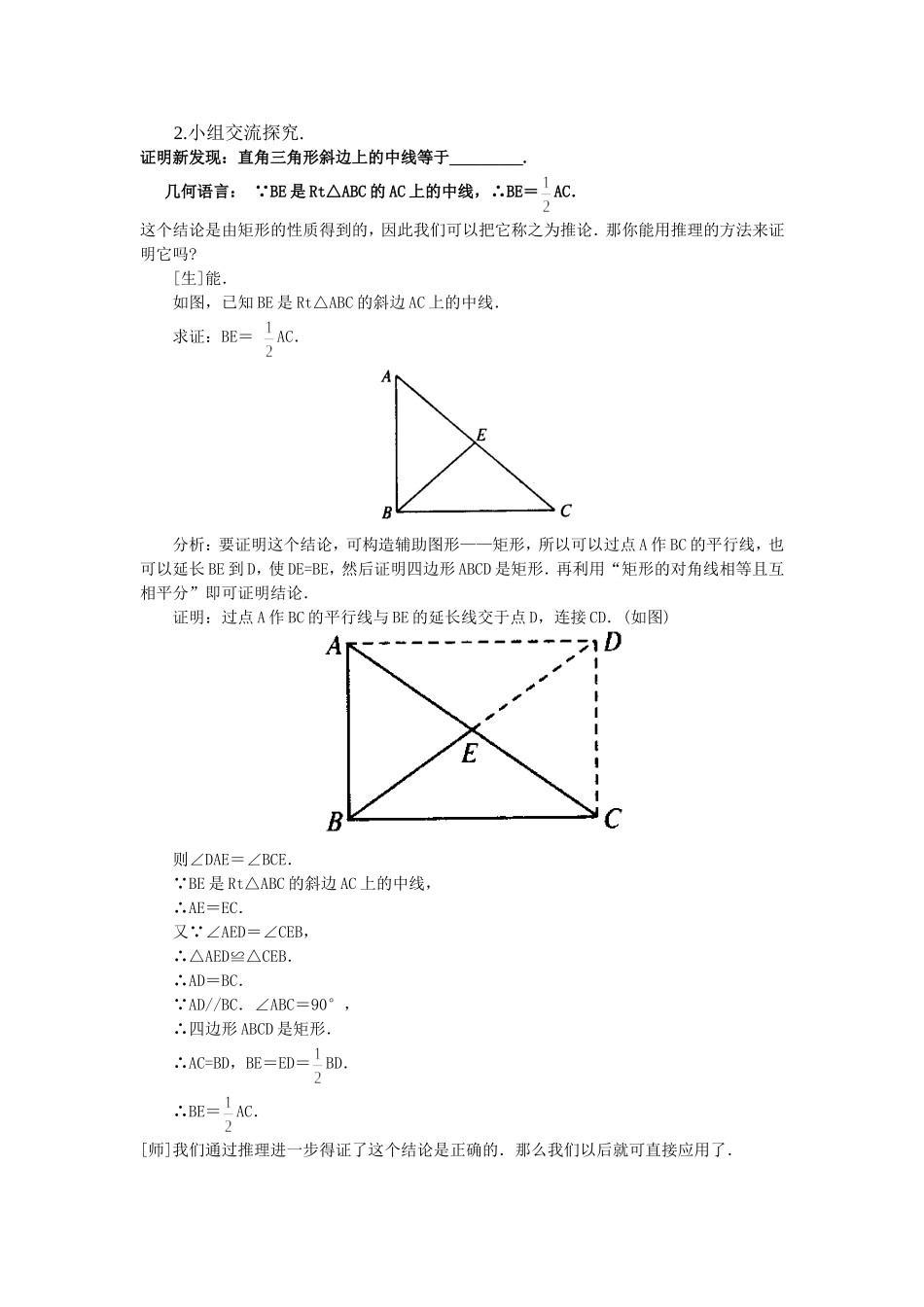
课题§3.2.1特殊平行四边形(一)——矩形兰州市第三十四中学李霞一、教学目标(一)知识与技能1.能用综合法来证明矩形的性质定理和判定定理以及其推论.2.能运用矩形的性质进行简单的证明与计算,解决相关实际问题(二)过程与方法1.经历探索、猜想、证明的过程,进一步发展推理论证能力.2.进一步体会证明的必要性以及计算与证明在解决问题中的作用.3.体会证明过程中所运用的归纳概括以及转化等数学思想方法.(三)情感与价值观要求1.通过学习矩形的性质,让学生从矩形与平行四边形的区别与联系中,体会特殊与一般的关系.2通过对定理的自主探究、验证,让学生获得亲自参与研究、探索的情感体验,增强学习数学的热情,感受证明的严谨性.教学重点矩形的性质的证明.教学难点矩形的性质的证明以及它与平行四边形的从属关系.教学方法启发引导归纳式教学法.教学用具活动的平行四边形二、教学过程(一)知识重现,导入新课.1.我们都知道三角形具有稳定性,平行四边形具有不稳定性.大家看:(师演示平行四边形的学具)当老师改变平行四边形的形状,(1)在变化过程中,这个四边形还是平行四边形吗?为什么?(是,两组对边分别相等的四边形式平行四边形)在这个过程中有哪些量发生了变化,哪些量没变?(2)当这个平行四边形有一个内角是直角时,平行四边形变成了我们非常熟悉的什么四边形?用一句话概括出矩形与平行四边形之间的关系_____________怎样的四边形是矩形?矩形的定义:有一个角是直角的平行四边形2.矩形既然是特殊的平行四边形,它就具有平行四边形的性质,同时又具有自己的特性。今天我们先来研究矩形的特殊性质.(板书课题)(二)推进新课.活动一:探索定理1.性质定理1:矩形的四个角都是直角.几何语言: 矩形ABCD,∴∠A=∠B=∠C=∠D=90°.(师生共析,学生总结给出证明过程)已知:四边形ABCD是矩形.求证:∠A=∠B=∠C=∠D=90°.证明: 四边形ABCD是矩形,不妨设∠A=90° 矩形ABCD是平行四边形∴∠A=∠C=90°又 AB//CD∴∠A+∠D=180°∠D=∠B=90°∴∠A=∠B=∠C=∠D=90°2.性质定理2:矩形的对角线相等.几何语言: 四边形ABCD是矩形,∴AC=DB.(师生共析,学生写出完整的证明过程)已知:矩形ABCD,求证:AC=DB.证明:在矩形ABCD中, ∠ABC=∠DCB=90°,(矩形的四个角都是直角)AB=DC,(平行四边形的对边相等)BC=CB,∴△ABC≌DCB.∴AC=DB.3、判定定理1:有三个角是直角的四边形是矩形.对于定理3,利用“同旁内角互补,两直线平行”证明平行四边形是比较简单的方法,如果学生采取其他方法,也应当鼓励。4、判定定理2:对角线相等的平行四边形是矩形.对于定理4,学生采取的方法大多利用全等三角形证明平行四边形某两个邻角相等,又互补从而推出直角,这里也要注意鼓励学生采取不同的方法证明。在证明过程中,对于重点步骤,应该要求学生写明理由,同时,还要关注学生的证明过程是否严谨清晰。活动二:定理的应用与拓展1.如图,设矩形的对角线AC与BD的交点为E.那么BE是Rt△ABC中一条怎样的特殊线段?BE与AC有什么大小关系?为什么?由此发现:直角三角形斜边上的中线与斜边存在怎样的关系?2.小组交流探究.证明新发现:直角三角形斜边上的中线等于_________.几何语言: BE是Rt△ABC的AC上的中线,∴BE=AC.这个结论是由矩形的性质得到的,因此我们可以把它称之为推论.那你能用推理的方法来证明它吗?[生]能.如图,已知BE是Rt△ABC的斜边AC上的中线.求证:BE=AC.分析:要证明这个结论,可构造辅助图形——矩形,所以可以过点A作BC的平行线,也可以延长BE到D,使DE=BE,然后证明四边形ABCD是矩形.再利用“矩形的对角线相等且互相平分”即可证明结论.证明:过点A作BC的平行线与BE的延长线交于点D,连接CD.(如图)则∠DAE=∠BCE. BE是Rt△ABC的斜边AC上的中线,∴AE=EC.又 ∠AED=∠CEB,∴△AED≌△CEB.∴AD=BC. AD//BC.∠ABC=90°,∴四边形ABCD是矩形.∴AC=BD,BE=ED=BD.∴BE=AC.[师]我们通过推理进一步得证了这个结论是正确的.那么我们以后就可直接应用了.(拓展运用)试写出上述命题的逆命题,并加以证...